Dichotomous Quasi-Rasch Model with Guessing

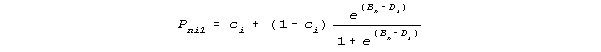
The standard dichotomous Rasch model does not incorporate guessing. Instead, guessing is detected as off-dimensional behavior by means of quality-control fit statistics. But for "minimum competency" tests guessing may need to be incorporated into the Rasch model as a lower asymptote to the item characteristic curve (ICC). In these circumstances, the guessability of an item is not a parameter to be estimated, but a constant to be specified. (In practice, the lower asymptote is specified as a constant in many supposedly 3-PL analyses.)

Here is a quasi-Rasch model (Keats' generalization) for guessing:

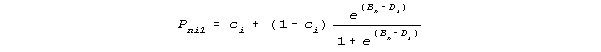
where ci is the probability of guessing the item, the lower asymptote to the ICC. This can be rewritten:

It is seen that when ci=0, this is the standard dichotomous model.

Estimation Equations

The slopes of the complementary ICCs are given by:

where Pnix is the probability that x = Xni = {0,1} is observed when person n encounters item i.

The likelihood of the data is:

The log-likelihood is:

Looking for the maximum-likelihood of the data across all values of the parameters, here for Bn:

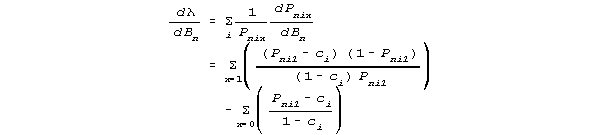
This does not have convenient sufficient statistics, except when ci=c, so that guessability is constant across items. But this is how many MCQ tests are intended to function.

When ci=c, then the maximum likelihood condition for Bn is:

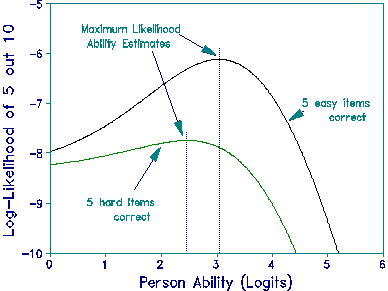
Maximum Likelihood Curves with Guessing

where Rn is the score for person n. There is a paradox here (and consequently also in 3-PL analyses). It is seen that, for a given raw score, success on easy items yields a higher estimated measure than success on hard items. The Figure shows this for a score of 5 right on a test of 10 items, uniformly distributed .1 logits apart, with guessability probability of .25.

The second derivative is, in general,:

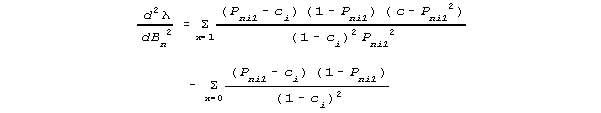
with the Newton-Raphson iteration equation:

John Michael Linacre

Colonius, H. (1977). On Keats' generalization of the Rasch model. Psychometrika, 42, 443-445.

Dichotomous Quasi-Rasch Model with Guessing. Linacre J.M. … 15:4 p. 856

Dichotomous Quasi-Rasch Model with Guessing Linacre J.M. … Rasch Measurement Transactions, 2002, 15:4 p. 856

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt154n.htm

Website: www.rasch.org/rmt/contents.htm