Judge Ratings with Forced Agreement

Many performance assessments have each piece of work rated by a pair of judges, supposedly rating independently. But a commonly applied rule is that, whenever the ratings awarded by the pair of judges differ by more than one category, that piece of work is rated by a third rater whose rating replaces that of the more discrepant of the original pair. Raters who are deemed discrepant too frequently are retrained and may be dismissed. The result is pressure on the judges to be "consistent", i.e., to conform to an imaginary consensus. The consequence of this pressure is a dataset in which the ratings of pairs of judges do not differ by more than one score-point for any piece of work. What are the measurement implications of this?

It is straightforward to construct a data matrix that accords with this intent. You can do it yourself. Imagine 7 pieces of work of increasing quality. These are the columns of the data matrix. Each is rated on a 1-6 rating scale. Each row of the data matrix is a judge, assigning ratings to each piece of work, but in such a way that the ratings of each piece of work (i.e., in each column) do not differ by more than one score-point. Your data matrix will look something like this:

1123456
1234566
2133456
1234455
1123456
1234566
1123456
1234566
1123456
1234566

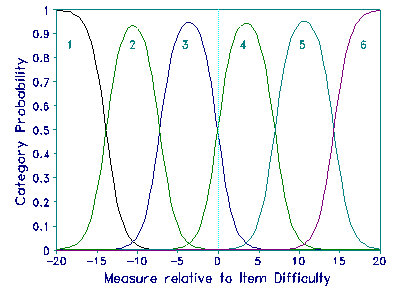
A Rasch analysis reveals the measurement implications of this forced agreement. The Figure depicts the category probability curves for the rating scale. The category curves display very little overlap with curves other than their immediate neighbors. For my dataset, the range of the scale is around 40 logits. This accords with the ranges of over 30 logits sometimes reported for assessments using this type of judging procedure.

What has happened? The attempt to increase reliability by forcing judge agreement has not worked as intended. Reliability is an ordinal or even, in the case of Cohen's Kappa, a nominal index. If the two judges were perfectly reliable, they would be like machines, always producing identical ratings. So they would act as one judge. We have here a variant of the "attenuation paradox" of raw-score classical test theory (CTT), or of what the legal profession "wood-shedding".

From the measurement perspective, each rating is expected to provide independent information about the location of the performance on the latent trait. It is the accumulation of that information, not the ratings themselves, that is decisive. Ratings which contradict the accumulated information certainly merit investigation, but are not automatically rejected. In the situation described here, the attempt to increase inter-rater reliability has actually reduced the independence of the judges, and so degraded the validity of the measures as measures.

John M. Linacre

Judge ratings with forced agreement. Linacre, JM. … 16:1 p.857-8

Judge ratings with forced agreement. Linacre, JM. … Rasch Measurement Transactions, 2002, 16:1 p.857-8

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt161a.htm

Website: www.rasch.org/rmt/contents.htm