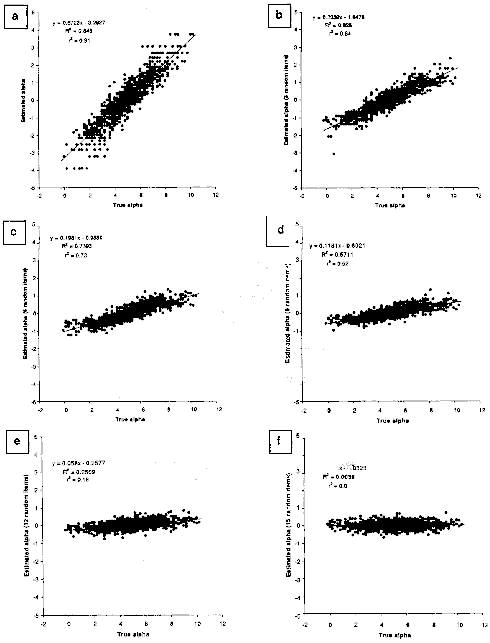
Massof (2002) Fig. 29 shows impact of random items on measurement . Courtesy: Optometry and Vision Science
Robert Massof's (2002) article in Optometry and Vision Science is a landmark in the history of Rasch measurement publishing, a virtual textbook on what measurement has been and could be. It comprehensively integrates Rasch-calibrated vision disability scales not only into the history of vision measurement, but into the historical role of measurement in both commerce and science. Massof provides excellent accounts of measurement from the perspectives offered by Likert, Thurstone, Classical Test Theory (CTT), IRT, and Rasch. His detailed examination of Likert's argument and method is priceless.
Massof's application of five criteria of fundamental measurement theory (additivity, double cancellation, solvability, the `all gaps are finite' Archimedean axiom, and independence) as a basis for model choice is an apparently independent development of the same argument recently presented by George Karabatsos (Bond & Fox, 2001, p. 195), and develops in greater detail the same arguments as those presented by Wright (1985, etc.). Like Karabatsos, Massof shows that the mathematical structure of the 2P IRT model violates each of the requirements for fundamental measurement.
Plots comparing Rasch and 2P IRT analyses of the same data show the results to be much more similar than is the case in my own recent explorations in this area, due in part to Massof's "fortuitous choice of a data set that minimized the differences between models (e.g., there was relatively little variation between items in the discrimination parameter of the IRT model, effectively making it a 'noisy' Rasch model)" (Massof, p. 538).
The article does not shy away from mathematical treatments and expositions of principle. It includes 33 equations, unusual for articles presenting measurement theory outside of technical psychometrics journals. Ten of the equations are associated with the IRT presentation, and 15 of them with Rasch models, and associated error, fit, and reliability statistics. Full credit is given where due, with extensive bibliographic citations (107 total) of Andersen, Andrich, Masters, Michell, Schulz, Smith, Wright, and others. Unfortunately, it appears that the article was in press when the Bond & Fox (2001) book came out, and so this resource is left unmentioned.
Empirical evaluations of statistics and models are the order of the day, with 37 numbered graphics in the article, the majority of which are scatterplots. The article includes a section focusing on Monte Carlo simulations that has the aim of demonstrating to the skeptic "that the Rasch model generates verifiable estimates of the latent variable." A data set of simulated observations from 1,000 respondents was designed from known values for 15 items, and was modified five times so as to include random responses for 3, 6, 9, 12, and all 15 items. The resulting calibrations and measures are plotted against their true values and against their fit statistics. Figure 29, reproduced from the article, shows the six plots of the measures versus their true values for each of the variations in the number of random items.
As expected, the scatterplots show a progressive movement away from 1) the identity line to a horizontal line centered at 0.0 logits for the comparisons of the calibrations and measures with themselves; and 2) a largely vertical spread to a horizontal line centered at 0.0 logits for the comparisons of the calibrations and measures with their fit statistics. The latter are interesting for their independent support for work by Richard Smith showing that misfitting anomalous responses are easiest to detect when the proportion of problematic items and/or examinee/respondents is low.
The standardized infit statistics for simulations with fewer random items easily isolate these "noisy" items at the high, positive end, but when there are more random items than not, the fit distribution settles right into the -2.0 to 2.0 range where one might think all is well (apart from the fact that the items all calibrate to 0.0). The results emphasize the value of strong theory and close study of construct validity, since random data are not likely to be produced from carefully designed questions asked of persons sampled from a relevant population.
The article briefly takes up some neglected history of Rasch applications to vision disability measurements, recounting the work of Wright, Lambert, and Schulz at Hines VA Hospital in the Chicago suburbs in the 1980s. Massof (p. 545) says:
"Like many other milestones in psychometrics, the use of Rasch analysis to measure vision disability can trace its origins to the University of Chicago. Georg Rasch was the father of Rasch analysis, but Benjamin Wright must be considered its legal guardian. Wright and his students and colleagues at the University of Chicago further developed and advanced Rasch's models, developed and validated analytic tools, and promoted and facilitated applications of Rasch models to a wide variety of fields."
Massof (p. 548) also makes brief notes of the convergence of different approaches to measuring visual abilities on a common construct, with the realization that the "different measurements can easily be transformed into a common unit."
The article concludes (p. 550) with strong statements on the value of Rasch measurement, statements that are supported by the thorough and extensive arguments and demonstrations presented:
"Many scientists have long been suspicious of the cavalier assertions by developers and users of visual function questionnaires that the average of patient ratings across questionnaire items is a valid measurement scale. With Rasch analysis, the validity of an instrument does not depend on inferential arguments and correlations with external variables. Rather, it exists on objective statistical tests of the model as an explanation of the data."
Massof's presentation of this work in the context of a field that has a long history of creating and maintaining reference standard metrics for its primary variables of interest bodes well for the extension of metrological networks away from their historical origins in the domains of physical variables into new homes in the domains of psychosocial variables. Those who act on the opportunity for the advancement of scientific and human values presented by the work of Rasch and others stand to make fundamental contributions. Massof's article will no doubt prove to be a powerful motivation to many who read it.
William P. Fisher, Jr.
Bond, T., & Fox, C. (2001). Applying the Rasch model: Fundamental measurement in the human sciences. Mahwah, New Jersey: Lawrence Erlbaum Associates.
Massof, R. W. (2002). The measurement of vision disability. Optometry and Vision Science, 79(8), 516-52.
Wright, B. D. (1985). Additivity in psychological measurement. In E. Roskam (Ed.), Measurement and personality assessment. North Holland: Elsevier Science.

Massof (2002) Fig. 29 shows impact of random items on measurement
. Courtesy: Optometry and Vision Science
The measurement of vision disability. Massof, R, Fisher WP Jr. … 16:2 p.874-6
The measurement of vision disability. Massof, R, Fisher WP Jr. … Rasch Measurement Transactions, 2002, 16:2 p.874-6
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt162c.htm
Website: www.rasch.org/rmt/contents.htm