The Standardization of Mean-Squares

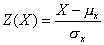
The reason for standardizing the infit and outfit mean square statistics is to allow their statistical significance, or p-values, to be more conveniently represented. A familiar scale to use for this purpose is the Z-scale, or standard normal scale. Most of us are familiar enough with this scale that we don't even need to look up the p-value of 1.96. And we know that a Z-score over 2.0 is "statistically significant." In contrast, one does not immediately know the statistical significance of variables from other commonly-used reference distributions, such as the chi-square distribution. The distribution changes with its degrees of freedom!

A general formula for converting a variable, X, to the standard normal variate, Z, is:

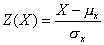(1)

Now one may be certain that Z(X) has a mean of 0 and a variance of 1, but unless X is normally distributed to begin with, the p-values of Z(X) in a standard normal distribution do not necessarily agree with the p-values of X in its own distribution. For instance, a "normally distributed" variable has no skew, but chi-square distributions are skewed.

Wilson & Hilferty (1931) found a way to transform a chi-square variable to the Z-scale so that their p-values closely approximated. Since chi-square distributions are skewed, the transformation has an extra layer of complexity. The first step in the transformation is to transform the chi-square statistic to a more normally-distributed variable. They showed that the pth root of a chi-square variable divided by its degrees of freedom, n, is approximately normally distributed and that

if		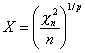(2)
then		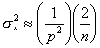(3)
and		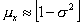(4)

Wilson & Hilferty chose p=3 (the cube root) for their transformation. The second step in the transformation is to substitute the results of Equations (2) through (4) into Equation (1). The complete transformation in terms of a chi-square variable, Y, with degrees of freedom, n, is:

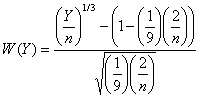(5)

Notice that Equation (5) has the basic form of a normalizing transformation, but is actually a normalizing transformation of a transformation! The p-values of W(Y) are very close to those of a standard normal variable, as desired. That is, if Z is a standard normal variable, P(Z < W(y)) approx. = P(Y < y). So W(Y) approximates a t statistic.

The expectation of a chi-square variable, Y, is its degrees of freedom n. So the expectation of Y/n is 1. Let's call this v_i. The model variance of Y is 2n. So the variance of Y/n is 2/n, let's call this q_i². Substituting in (5) and simplifying, we can see that (5) parallels the formula for the standardized weighted mean square at the bottom of Table 5.4a in Rating Scale Analysis (Wright & Masters, 1982, p. 100):

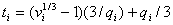(6)

In RSA, the residuals comprising the v_i have been weighted, embodying an unstated assumption that the distributional characteristics of weighted and unweighted mean-squares are the same. The unweighted form, which matches (5) exactly, substitutes u_i for v_i and the unweighted mean-square variance for the weighted one. Since the actual degrees of freedom for residual chi-squares are difficult to compute, RSA estimates them from the model distributions of the observations.

Matthew Schulz

Wilson, E. B., & Hilferty, M. M. (1931). The distribution of chi-square. Proceedings of the National Academy of Sciences of the United States of America, 17, 684-688. water.usgs.gov/osw/bulletin17b/Wilson_Hilferty_1931.pdf

Standardization of mean-squares. Schulz, M. … 16:2 p.879

Standardization of mean-squares. Schulz, M. … Rasch Measurement Transactions, 2002, 16:2 p.879

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt162g.htm

Website: www.rasch.org/rmt/contents.htm