Random Effects Rasch Model

Georg Rasch was concerned to construct measurement models with "parameters that are specific to the individuals" (1960, p. 9). An early extension of the Rasch model specified that the "individuals" were to be treated as random variables drawn from some distribution. This is now done routinely using the PROX algorithm and Marginal Maximum Likelihood Estimation MMLE.

Lalitha Sanathanan in "Some Properties of the Logistic Model for Dichotomous Response" (JASA, 69, 347, 744-749, 1974!) attempts this, but immediately encounters a major hurdle, the multiplicative form of the Rasch model then in common use. After Herculaean effort, she derives a simple approximation, but is forced to present it in additive form in order to make it tractable. Rewritten, the approximation is:

where N is the sample size, S_i is the number of correct answers to item i, and D_i is the difficulty of item i. α and β are sample dependent, but how they relate to the mean and standard deviation of the distribution is omitted from the paper. In fact, this formulation is equivalent to the PROX equation for a sample distributed N(μ,σ²), when

and

Sanathanan realizes that she has "shown how the parameters in the model can be calculated in a rough ready manner" (p. 749), but the utility of her insight was lost due to her abstruse math.

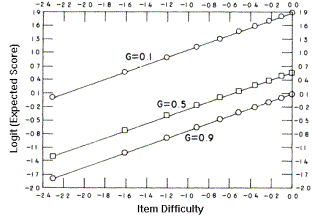
Sanathanan's plot of expected score against item difficulty for different sample distributions.

Random effects Rasch model. Sanathanan, L. … Rasch Measurement Transactions, 2002, 16:2 p.881

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt162i.htm

Website: www.rasch.org/rmt/contents.htm