Expected A Posteriori (EAP) Measures

Under Rasch model conditions, there is some probability that a person will succeed or fail on any item, no matter how easy or hard. This means that there is some probability that any person could produce any response string. Even the most able person could fail on every item.

The measure estimated for a person is usually that for which the observed response string is most likely, or that for which the response string best fits a Rasch model. We may, however, have some rough idea about a person's ability measure (or an item's difficulty) prior to the current data collection and wish to incorporate this idea into the newly estimated measure. To do this, we calibrate the test items in the usual way. Then we combine the item calibrations, our prior rough idea, and the observed responses to obtain an improved, a posteriori, person measure. Mislevy and Stocking (1989) recommend this approach for IRT models. John Uebersax (1993 and on his website) outlines a general procedure for this.

The technique capitalizes on an insight of Thomas Bayes:
Prior Probability x Data Probability => Posterior Probability

which implies that
Prob (B' given {X}) =
Prob (B' ) x Prob ({X} given B' ) / Sum over all B [ Prob (B) x Prob ({X} given B) ]

where B' is a particular value of the person measure, and the sum is over all possible values of our rough idea, B. {X} is the person's response string. The EAP estimate of the person measure is the expected value of this:
EAP estimate = Sum over all B [B x Prob (B given {X})].

Thus, suppose that our rough idea, the prior distribution of B, φ(B), is a convenient distribution, such as N(μ,σ²). The test consists i=1,L items. P_Xni is the probability of person n of ability B scoring X_ni on item i.

EAP estimates may be more central or more diverse than MLE estimates depending on the choice of prior distribution.

Then

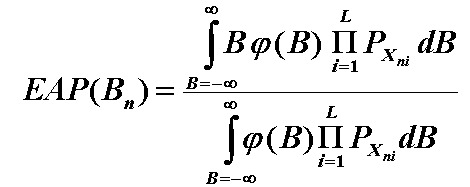
This can be evaluated using numeric quadrature to approximate the integrals.

John M. Linacre

Mislevy RJ & Stocking ML (1989) A consumer's guide to LOGIST and BILOG. Applied Psychological Measurement, 13, 57-75.

Uebersax JS (1993) Statistical modeling of expert ratings on medical treatment appropriateness. Journal of the American Statistical Association, 88, 421-427.

Expected A Posteriori (EAP) Measures. Uebersax JS. … 16:3 p.891

Expected A Posteriori (EAP) Measures. Uebersax JS. … Rasch Measurement Transactions, 2002, 16:3 p.891

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt163i.htm

Website: www.rasch.org/rmt/contents.htm