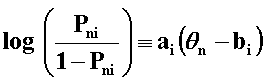
The dichotomous Rasch model specifies that all items have the same discrimination. But what happens if that discrimination is zero? Some critics perceive here a flaw in the Rasch model (e.g., Bollinger & Hornke, 1978), but, paradoxically, the Rasch model analysis is accurate. It is the 2-PL analysis that is flawed!
Here is a 2-PL IRT model including its usual item discrimination parameter, ai:
|
|
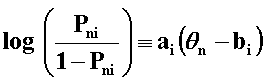
If all item discriminations are the same, ai=a and this becomes a Rasch model. Thus data which fit a 2-PL model with uniform item discriminations also fit a Rasch model with Rasch parameters Bn = a.θn and Di = a.bi. This presents no conceptual difficulties except in the case of a = 0. A 2-PL analysis would, one imagines, report that a = 0, but the Rasch analysis cannot do this, so what would it report?
If all ai=0 in the 2-PL model statement above, then Pni = 0.5 for all n and i. So that, from the Rasch perspective, all Bn = B and all Di = D, and B = D. This is equivalent to coin-tossing. The Rasch analysis would unambiguously report that all person abilities equal all item difficulties, and the data would fit the Rasch model.
In fact, a Rasch analysis can go further. If the items are not discriminating, so that Bn = B and Di = D, but B><D, then this is equivalent to tossing a biased coin. B-D is a measure of the bias in the coin. Rasch would report correctly that all person abilities are equal, and that all item difficulties are equal, but that person ability is unequal to item difficulty. The data would fit the model.
With a biased coin, 2-PL estimation algorithms encounter a paradox. If item discrimination dominates, then ai=a=0 is reported, but the resultant model does not fit the data. This is because a=0 implies Pni=0.5, but in fact Pni><0.5.
If ability and difficulty dominate, then θn = θ and bi = b and ai = a = 1 (or a constant, not equal to 0). The model does fit the data, but 2-PL now misreports the uniform zero discrimination as non-zero! In a situation in which the Rasch measures are straightforward to interpret, it is the 2-PL estimates that are either incorrect or misleading.
John M. Linacre
Bollinger G & Hornke L.F. (1978) The relationship between item discrimination and Rasch scalability. [German]. Archiv für Psychologie, 130, 89-96
The Zero-Discrimination Paradox. Linacre, JM. … Rasch Measurement Transactions, 2003, 16:4 p.904
| Rasch Publications | ||
|---|---|---|
| Rasch Measurement Transactions (free, online) | Rasch Measurement research papers (free, online) | Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch |
| Applying the Rasch Model 2nd. Ed., Bond & Fox | Best Test Design, Wright & Stone | Rating Scale Analysis, Wright & Masters |
| Introduction to Rasch Measurement, E. Smith & R. Smith | Introduction to Many-Facet Rasch Measurement, Thomas Eckes | Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr. |
| Statistical Analyses for Language Testers, Rita Green | Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar | Journal of Applied Measurement |
|
|
|
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| May 15-17, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| May 20-22, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| May 31 - June 28, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 7, 2013, Fri. | SPHERE workshop: Response-Shift and subjective measures in health science, Nantes, France, www.sphere-nantes.fr/ |
| June 19-21, 2013, Wed.-Fri. | SIS 2013 Conference on Advances in Latent Variables: Methods, Models and Applications, Brescia, Italy, meetings.sis-statistica.org/index.php/sis2013/ALV |
| July 1 - Nov. 30, 2013, Mon.-Sun. | Online Course: Introduction to Rasch Measurement Theory (D. Andrich, RUMM), uwa.edu.au |
| July 5 - Aug. 2, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| Aug.1-5, 2013, Thur.-Mon. | TERA-PROMS Annual Meeting, Kaohsiung, Taiwan, tera.education.nsysu.edu.tw |
| Aug. 9 - Sept. 6, 2013, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Aug. 22, 2013, Thursday. | Symposium in honor of Svend Kreiner, Copenhagen, Denmark, biostat.ku.dk/kreinersymposium |
| Sept. 4-6, 2013, Wed.-Fri. | IMEKO TC1-TC7-TC13 Symposium: Measurement Across Physical and Behavioural Sciences, Genoa, Italy, www.imeko-genoa-2013.it |
| Sept. 13 - Oct. 11, 2013, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 18-20, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 23-25, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 26-27, 2013, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Oct. 18 - Nov. 15, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Oct. 20 - Oct. 25, 2013, Sun.-Fri. | International Association for Educational Assessment (IAEA) 39th Annual Conference, Tel Aviv, Israel, www.iaea-2013.com |
| Dec. 11-13, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| March 12-14, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| May 14-16, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| May 19-21, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| July 4 - Aug. 1, 2014, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| Aug. 8 - Sept. 5, 2014, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Sept. 10-12, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 12 - Oct. 10, 2014, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 15-17, 2014, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 18-19, 2014, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| The javascript to add "Coming Rasch-related Events" to your webpage is: <script type="text/javascript" src="http://www.rasch.org/events.txt"></script> | |
The URL of this page is www.rasch.org/rmt/rmt164h.htm
Website: www.rasch.org/rmt/contents.htm