Item Information: When Gaps Can Be Bridged

Fit of data to the Rasch model always makes us feel comfortable. While fit provides evidence of accuracy of the measurement model of the variable of interest, precision, however, is a different issue, namely the issue of targeting. (Strictly speaking, mistargeting also affects the power of the test of fit.) If items are operational in a range of the latent dimension but most of the respondents are located in a different range, person (and item) parameter estimates lack precision and standard errors are large. The reason, of course, is that the further apart an item and a person is, the less information the item provides about the location of the person, with item information being calculated as P*(1-P) (Fischer, 1974, p.294). Over the items in a test, individual item information adds up to test information (Fischer, 1974, p.296). The test information curve typically but not necessarily is bell-shaped with its maximum at 0 (provided the scale has been defined by the sum of items equal to 0).

An interesting variant of mistargeting occurs when items are clustered in terms of their location and most or many persons are between the clusters (see Figure 1).

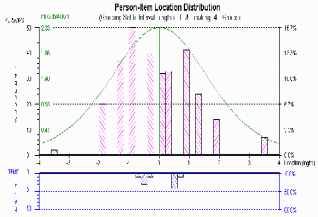
Figure 1: Distribution of Person and Item Locations (Produced by RUMM2020 (Andrich et al., 2003), simulated data)

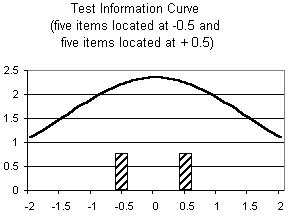
Figure 2: Test Information Curve for five items located at -0.5 and five items located at + .5.

Figure 3: Test Information Curve for five items located at -1.5 and five items located at + .1.5.

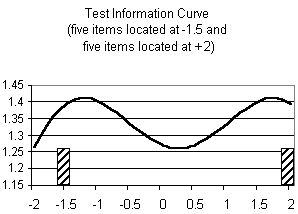
Figure 4: Test Information Curve for five items located at -1.5and five items located at + 2.0.

Let us assume that, for simplicity, in a ten item test, five dichotomous items are located exactly at -0.5 and five other items are located at 0.5 on a logit scale. (Assuming that there are no further items below -.5 and above +.5 does not have a substantial impact on the conclusions drawn.) In other words, there is a gap between these item clusters. Intuitively, one might think that information is higher at -0.5 and at 0.5, respectively, than between -0.5 and 0.5 due to the gap between item locations. However, in most cases, the gap between items does not imply less information. On the contrary, information peaks out right in the middle of the gap, i.e. at 0 (with 2.35 of total test information in the given example). At the centers of either item cluster, information only amounts to 2.23 (see Figure 2).

The explanation is that, though, information reaches its maximum at ξ (person ability) = δ (item difficulty) with .5 * (1 - .5) = .25, it remains rather high over a relatively wide range. At |ξ - δ| = .5 it still is .235 and at |ξ - δ| = 1 it amounts to .197. While information is reduced when moving from ξ = δ to |ξ - δ| = 1 by .053 points, the rate of decrease almost doubles for a further logit unit between x and d with information being only .105 at |ξ - δ| = 2. Consequently, in our example, when moving from -.5 into the gap between -.5 and +.5 we loose information provided by the items clustered at -.5. But at the same time we gain information by the items clustered at +.5. For a person location of, e.g., -.2 we loose .006 per item clustered at -.5 whereas we gain .025 from items located at +.5, i.e. four times as much. In other words, total information increases. Thus, we get the same bell-shaped information curve even though there is a gap. It should be noted that in terms of interpretation of person locations within the gap, the lack of items located in this range is certainly not satisfactory.

It is interesting to compare the situation with a Guttman scale. If the items would function perfectly all persons within the gap would get all the five items at -.5 right and all the five items at +.5 wrong. There would be no way to tell whether a particular person is closer to -.5 or to +.5. So, it is the stochastic uncertainty under the Rasch model, the "imperfect nature" so to speak, that yields information and, as a consequence, precision.

However, not all gaps can be bridged. If the distance between the item clusters is too large, the loss of information from "near" items when moving into the center of the gap is not compensated for by the gain of information from "distant" items. The result is a double-peaked total information curve (see Figures 3 and 4).

Thomas Salzberger Vienna University of Economics and Business Administration, Austria

The author wants to thank Alan Tennant (University of Leeds) and David Andrich (Murdoch University) for the stimulating input they provided.

Andrich, D.; Lyne, A.; Sheridan, B.; Luo, G. (2003): RUMM2020, v. 4.0, Rumm Laboratory.

Fischer, Gerhard (1974): Einführung in die Theorie psychologischer Tests [Introduction to the Theory of Psychological Tests], Huber, Bern.

Item Information: When Gaps Can Be Bridged. Thomas Salzberger … Rasch Measurement Transactions, 2003, 17:1, 910-911.

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt171h.htm

Website: www.rasch.org/rmt/contents.htm