Item Specification vs. Item Banking

Our thesis is simple and straightforward. It is not necessary to have a bank of items for measuring a construct when we possess an algorithm for writing an item at any desired level of difficulty. The algorithm is the key to the bank, so to speak. If one has the key, the bank is open.

Bruce Choppin (1968) was an early Rasch pioneer who promoted item bank development. Items representative of the variable of interest are banked and selected for use as required. Leveled paper-pencil tests can be quickly assembled from the bank of items based on their associated item calibrations and item use histories. Also, computer based adaptive tests can be assembled electronically and targeted to each examinee. As useful as item banking has proven to be it is possible to move beyond the banking of individual items and their associated item statistics.

When enough is known about what causes item difficulty a specification equation can be written that yields a theory based item calibration for any item the computer software designs. An item's calibration is seen to be the consequence of decisions the computer software makes in constructing the item. This process mimics the steps a human item writer takes in constructing an item, albeit, with more control over the causal recipe for item difficulty. A thesis of this paper is that when asserting that a measure possesses construct validity there is no better evidence than demonstrated experimental control over the causes of item difficulty.

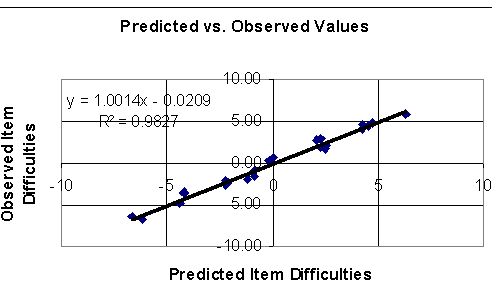
A measurement instrument embodies a construct theory; a story about what it means to move up and down a scale (Stenner, Smith & Burdick, 1983). Such a theory should be vigorously tested. In a demonstration of these methods Stone (2002) theorized that the difficulty of short term memory and attention items (Knox Cube Test) was caused by (1) number of taps, (2) number of reverses in the direction of the tapping pattern and (3) total distance in taps for the pattern. This theory was tested by regressing the observed item difficulties on the above mentioned three variables. The Figure plots the correspondence between predicted (theoretical) item difficulties and observed item difficulties. Ninety-eight percent (98%) of the variation in observed item difficulties was explained by number of taps (standardized Beta=.80) and distance covered (standardized Beta=.20). Number of reverses in the context of these two predictors made no independent contributions. An earlier study (Stenner and Smith, 1982) using different samples of items and persons found that an equation employing the same two variables explained 93% of the item difficulty variance. Finally, Stone (2002) re-analyzed KCT-like items developed over the last century and found a striking correspondence between the two variable theory and observation. We should note that there is some uncertainty in the observed item difficulties analyzed in these studies, suggesting that the disattenuated correlation between theory and observation approaches unity.

When item difficulties and by implication person measures are under control of a construct theory and associated specification equation it becomes possible to engineer items on demand. No need to develop more items than you need, pilot test these items, estimate item calibrations and then bank the best of these items for use on future instruments. Rather, when an instrument is needed an algorithm generates items to a target test specification along with calibrations for each item.

Applications that incorporate the above ideas are under development for the next KCT revision and for an on line reading program that builds reading items real time as the reader progresses through an electronic text.

Some of the practical benefits of what might be called theory referenced measurement are (1) if the process yields reproducible person measures, then evidence for construct validity is strong, (2) test security is facilitated because there are no extant instruments that would be compromised upon release, and (3) a fully computerized procedure keeps the process under tight quality control at a fraction of the cost of traditional item standardization procedures.

Finally, one well-recognized means of supporting an inference about what causes item difficulty is to experimentally manipulate the variables in the specification equation and observe whether the predicted item difficulties materialize when examinees take the items. In building the latest version of the KCT a part of the scale had an insufficient number of items. The specification equation was used to engineer candidate items to fill in the space. Subsequent data collection confirmed that the items behaved in accord with theoretical predictions (Stone, 2002). Although this exercise involved only four items, it suggests that the construct specification equation is a causal representation (rather than merely descriptive) of the construct variance.

Reflecting on this extraordinary agreement between observation and theory suggests two conclusions: (1) the specification equation affords a nearly complete account of what makes items difficult, and (2) the Rasch model used to linearize the ratios of counts correct/counts incorrect must be producing an equal interval scale or a linear equation could not account for such a high proportion of the reliable variation in item difficulties.

Measurement of constructs evolves along a predictable course. Early in a constructs history measurements are subjective, awkward to implement, inaccurate and poorly understood. The king's foot as a measure of length is an illustration. With time, standards are introduced, common metrics are imposed, artifacts are adopted, (e.g. the meter bar) precision is increased and use becomes ubiquitous. Finally, the process of abstraction leaps forward again and the concrete artifact based framework is left behind in favor of a theoretical process for defining and maintaining a unit of length (oscillations of a cesium atom). Human science instrumentation similarly evolves along this pathway of increasing abstraction. In the early stages a construct and unit of measurement are inseparable from a single instrument. In time multiple instruments come to share a common metric, item banking becomes commonplace and finally, the construct is specified. When a specification equation exists for a construct and accounts for a high percentage of the reliable variance in item difficulties (or ensembles) the construct is no longer operationalized by a bank of items but rather by the causal recipe for generating items with pre-specified attributes.

Jack Stenner & Mark Stone

Choppin, B. (1968). Item banking using sample-free calibration. Nature, 219 (5156), 870-872.

Stenner, A. J. & Smith, M. (1982). Testing construct theories. Perceptual and Motor Skills, 55, 415-426.

Stenner, A. J., Smith, M. & Burdick, D. S. (1983). Toward a theory of construct definition. Journal of Educational Measurement, 20 (4), 305-315.

Stone, M. H. (2002). Quality control in testing. Popular Measurement, 4 (1), 15-23.

Stone, M. H.(2002). Knox's cube test - revised. Wood Dale: Stoelting.

Item Specification vs. Item Banking, Stenner A.J. & Stone M.H. … Rasch Measurement Transactions, 2003, 17:3 p.929-930

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt173a.htm

Website: www.rasch.org/rmt/contents.htm