Test Validity and Rasch Measurement: Construct, Content, etc.

Early in his career, Lee J. Cronbach made a perceptive statement, "A test is valid to the degree that we know what it measures or predicts" (1949, emphasis his). In the ensuing 50 years, test validity has become an evermore complex topic. Here is an interpretation of Sam Messick's (1989 etc.) conceptualization:

		Purpose
		Interpretation	Use
Justification	Evidence	Construct validity Content validity Face validity	Utility Predictive validity Concurrent validity Criterion-oriented validity Statistical reliability
	Consequence	Value implications	Social consequences

Rasch measurement, as a means of test analysis, parallels physical measurement processes. Both are largely concerned with the construction of accurate, precise, linear measures along specific, unidimensional constructs. Even in those instance when a multi-dimensional Rasch approach is employed, the assumption is that the multi-dimensional space is a composite of unidimensional variables.

Consider the beginning of large-scale precise and accurate physical linear measurement for industrial purposes. This was an accomplishment of F. A. Pratt and Amos Whitney in the 1870s. But were their "comparator" and its resultant "standard inch" valid as a "test of length"? Not according to Messick's summary, because early applications were to the manufacture of military equipment including German Mauser rifles and British naval guns. Thus the "comparator" facilitated the carnage of the First World War. Its social consequences were dire. Surely Pratt and Whitney should have abandoned their project! But then the modern age of precision technology, mass production, speedy transportation and computers might never have occurred. Should development of tests of literacy be abandoned because such tests have been used to disenfranchise the illiterate? Surely it is impossible for a Test Constructor to predict the social consequences of a Test in any other than a short-sighted and limited way.

The value implications of a bathroom weight-scale can also be profound. Low numbers possibly indicate anorexia, high numbers probably indicate obesity. Both of these have negative stereotypical implications, i.e., detrimental value implications.

In Messick's scheme, uses and consequences, even when intended, recommended or foreseen by the constructor, are largely beyond the constructor's control. Only the "construct validity" cell is strictly within the control of the Test constructor.

The motivation for test construction comes from its hoped-for consequences. Those consequences suggest a Test's intended uses. But the history of science indicates that actual uses can be far wider than those original intended uses. Newton's Laws of Motion originated in astronomy. Computers were not conceptualized as a means of entertainment.

Content validity is an initial screening device. It verifies that extraneous material has been omitted, and that the test is representative of all relevant material. The history of the development of the thermometer indicates that the definition of what is relevant content can change as test development progresses. Thermometry now encompasses measuring the temperature of stars, but now excludes the impact of atmospheric pressure. Careful development of an educational achievement test may identify both gaps and irrelevancies in the material being taught.

Rasch measurement produces a hierarchy of persons along the latent variable. Are those persons regarded as high performers at one end of the hierarchy, and those regarded as low performers at the other with a gradation in between? If so, this indicates "Use-Evidence" of validity (predictive, concurrent, criterion-oriented, etc. - depending on the source of the external information about the sample.) But samples have their idiosyncrasies, as do external indicators, so, more important is ...

The hierarchy of items along the latent variable. This is the progression from "easy" to "hard", "common" to "rare", "general" to "specific", etc. Before (or without knowledge of specific details of the) data collection, experts should predict the difficulty ordering of the items (according to the intended construct theory). This is then compared with the items' empirical difficulties. Coincidence confirms construct validity as demonstrated in the books by Wright & Masters' (1982) "Rating Scale Analysis" and also Wright & Stone' (1979) "Best Test Design". Correlations are not important here (but can be computed, if desired). More important is that empirical disordering of one or more items in the overall hierarchy indicates that those particular items may be exhibiting unintended features - or that the construct theory is deficient.

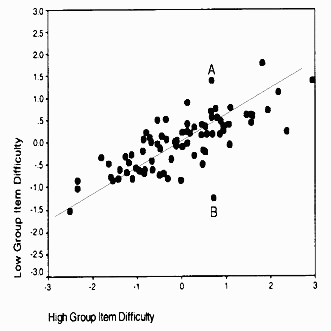
Figure 1. High group vs. low group item difficulty. (Smith & Suh, 2003, Journal of Applied Measurement 4:2, 159)

Figure 1 is illustrative of the investigation of construct validity. It is typical of scatterplots of item difficulties for Pre-test and Post-test administrations, or at-Admission and at-Discharge. In the Figure, the item spread is wider for the high group (6 logits) than for the low group (4 logits). So the high group discriminate item difficulty more strongly. This is typical of educational tests, e.g., of Chinese characters, where, as knowledge increases, the difference between easy and hard items becomes more pronounced. Quality-of-life assessment during rehabilitation shows the opposite characteristic. As patient status returns to normal, all regular tasks become equally easy. The variable defined by the widest spread of item difficulty is usually the most relevant.

In Figure 1, however, two somewhat different variables have been defined. For the high group, items A and B are equally difficult. For the low group, those same items A and B are almost at the extremes of the variable as defined by these items. Which is the intended variable? If the order of items had been predicted a-priori according to some construct theory, then the hierarchy more closely matching the intended variable could be identified immediately. The best result, from a construct validity perspective, would be that the intended variable follows the "best fit" diagonal line on the plot. Since items A and B are so markedly misplaced, it is likely that they contain flaws or features which make them essentially different items for the two performance groups. Construct validity must be carefully constructed, it is unlikely to emerge fortuitously from a collection of test items.

John Michael Linacre

Messick, S. (1989). Validity. In R.L. Linn (ed.) Educational measurement. Third edition. New York: Macmillan, 13-103.

Smith R.M. & Suh K.K. (2003) Rasch fit statistics as a test of the invariance of item parameter estimates. Journal of Applied Measurement, 4:2, 159.

Test Validity and Rasch Measurement: Construct, Content, etc., Linacre J.M. … Rasch Measurement Transactions, 2004, 18:1 p.970-971

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt181h.htm

Website: www.rasch.org/rmt/contents.htm