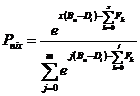 (1)
(1)At least one aspect of Rasch measurement continues to perplex analysts and paper reviewers. Are Masters' Partial Credit Model and Andrich's Rating Scale Model variants of the same polytomous model or different models?
The Andrich (1978) Rating Scale Model conceptualizes all items on an instrument to share the same m+1 ordered-category rating scale:
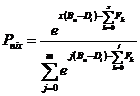 (1)
(1)
with the usual parameterization, where x=0,m and F0=0
or any
convenient constant, also ![]() = 0.
= 0.
The Masters' (1982) Partial Credit Model conceptualizes each item to exhibit a unique rating scale structure of mi+1 ordered categories.:
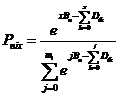 (2)
(2)
where x=0,mi and Fi0=0 or any convenient constant.
In many survey instruments, subsets of items share rating scales, some items have unique rating scales, and some items are dichotomies. The generalization of the Andrich Rating Scale Model to groups of items encompasses all these:
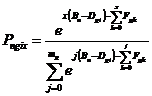 (3)
(3)
where g indicates the group of items (sharing the same rating scale structure) to which item i belongs. This is called the "Grouped Rating-Scale Model".
But what if every group contains only one item? Then g has the same meaning as i, and this model becomes:
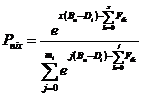 (4)
(4)
Now it appears that there are two different Rasch models for the
identical situation: the "Partial Credit" and the "One-Item Rating
Scale". What is the relationship between them? Let us take the
Partial Credit model and reparameterize Dik as
bi + τik where
![]()
Then,
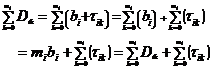 (5)
(5)
Therefore,
![]() which is the same constraint as in the one-item
rating scale model.
which is the same constraint as in the one-item
rating scale model.
Thus, the difference between the two models is reduces to parameterization. The "Partial Credit" Dik is identical to the "one-item Rating Scale" Di + Fik as constrained by
![]() and
and
![]() (6)
(6)
Consequences of this equivalence include the definition of an overall "item difficulty" for a Partial Credit item as Di, and also any theoretical properties or practical implications obtained for one model can be carried directly over to the other.
Di has a convenient interpretation: it is the location (i.e., person measure) on the latent variable at which the highest and lowest category are equally probable. To confirm this, let Bn be the ability of person n with equal probability of being observed in the lowest and highest categories of item i of difficulty Di:
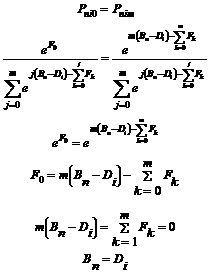 (7)
(7)
Thus item difficulty for Andrich's Rating Scale model and Masters' Partial Credit model can have the same definition. The models are equivalent.
John Michael Linacre
Andrich D. (1978) A rating scale formulation for ordered response categories. Psychometrika, 43, 561-573.
Masters G.N. (1982) A Rasch model for partial credit scoring. Psychometrika, 47, 149-174.
The Partial Credit Model and the One-Item Rating Scale Model, Linacre J.M. … Rasch Measurement Transactions, 2005, 19:1 p. 1000-1002
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt191e.htm
Website: www.rasch.org/rmt/contents.htm