Software demonstration of the bootstrap application to conditional item difficulty parameters in Rasch

 

                                                     Kingsley E. Agho

Centre for Clinical Epidemiology and Biostatistics

University of Newcastle,

                                                         James A. Athanasou

                                                     Faculty of Education

                                                University of Technology, Sydney

 

Abstract

A brief overview of the Rasch conditional logit item difficulty parameter is provided. Next we demonstrate two statistical software procedures for estimating the bootstrap application of the Rasch conditional logit item difficulty parameter to teachers and Rasch users with little programming skills. Finally, we propose that the bootstrap software demonstrate here will provides Rasch users with more than one way of investigating research question in educational testing.

Kingsley E. Agho

Centre for Clinical Epidemiology and Biostatistics (CCEB),

The University of Newcastle,

Level 3, David Maddison Building,

Royal Newcastle Hospital,

NSW 2300, Australia.

 

 

Introduction

            The bootstrap method was first introduced to statistics by Efron (1979) as a general method for estimating standard errors and bias of parameters in statistical models. The bootstrap technique has become increasingly popular in educational testing because it provides researchers with more than one way of investigating research questions and we will demonstrate the bootstrap software application to conditional Rasch item difficulty parameter later.

            In general, the bootstrap application to the Rasch measurement model seeks to provide a better understanding of what parametric Rasch models do. It is based on the rationale of no assumption about the population from which either items or persons are sample; and, offers procedures for data with much smaller numbers of items and persons. However, to the best of our knowledge, existing Rasch measurement software cannot apply the bootstrap method.

            The aim of this short communication is to provide two different (R and Stata) statistical packages for estimating bootstrap applications in Rasch conditional item difficulty parameters to teachers and Rasch users with little programming skills. The R-statistical software is available for free (www.r-project.org).

 

Conditional Item Difficulty Estimates in Rasch

            In this short communication, the item parameter will be used to refer to as b. Consider the following response data situation, where  represents dichotomous responses given to j items. Let  be the binary or dichotomous  (1,0) response for person (= 1,…,N) and item j (j = 1,…n), where 1 denotes a correct response and 0 denotes an incorrect response. Let and . The simplest and the most widely quoted model for  is the Rasch model (Rasch, 1960) and the Rasch conditional logistic model (T_i|j) is:

 

T_i|j = ln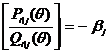                                                                            (1) 

 

where  is the person ability parameter and b_j is the item parameter. 

 

Data Structure

            Before the use of the software packages are explained, the set-up of the data into a readable format needs to be discussed. For example, a typical dichotomous data structure on five individuals on three dichotomously-scored test items is given in column 1-4 of Table 1. To estimate conditional item difficulty parameters, the data is reshaped lengthwise and the expression in (1) will be used to create a dummy variable Th's which represents - b_j or the betas in (1) (see column 5-10 in Table 1) and the conditional logistic function was used to estimate the Rasch difficulty parameter.

 

Table 1

 

Illustration of Data format for readable Data and Rasch item difficulty estimate.

Data Format				Rasch Item difficulty Estimate Data format
student_id	Ques1	Ques2	Ques3		student_id	item	Ques	Th1	Th2	Th3
1	1	0	0		1	1	1	-1	0	0
2	0	0	0		1	2	0	0	-1	0
3	0	0	1		1	3	0	0	0	-1
4	1	0	1		2	1	0	-1	0	0
5	0	1	0		2	2	0	0	-1	0
					2	3	0	0	0	-1
					3	1	0	-1	0	0
					3	2	0	0	-1	0
					3	3	1	0	0	-1
					4	1	1	-1	0	0
					4	2	0	0	-1	0
					4	3	1	0	0	-1
					5	1	0	-1	0	0
					5	2	1	0	-1	0
					5	3	0	0	0	-1

Note: For R-statistical software, Ques = resp, student_id = id and Th = i.

 

Software package demonstration and sample output

            Two statistical software packages have been selected for illustration in this short communication. The first package is the comprehensive public domain R statistical software and secondly the commercial Stata statistical package. The dataset used in this demonstration consisted of 200 individual's responses to 10 dichotomously-scored examination questions. In both cases (R and Stata) each of the 10 items is replicated 1000 times to give the bootstrap estimate while item 10 is the reference level when the conditional logistic Rasch method is applied.

            To apply the bootstrap method to the conditional Rasch item difficulty parameters, we used Davison and Hinkley's (1997) boot library in R-statistical software. In the boot function, "statistic" is a function that returns the statistic to be bootstrapped. The first two argument of the function "boot.cond" specified the reshaped data set "combine" and the index vector gives the indices of the observations included in the bootstrap sample while "R" is the number of bootstrap replicates. The sample output is shown below. A complete step-by-step guide for users unfamiliar with the R package is available form the author upon request.

 

            In the Stata example, we build upon the programming written by Weesie in 1997. "bs" is the bootstrap sample while "reps"  is the number of bootstrap replicates. In most bootstrap applications, an investigation using a B=1000 bootstrap sample will essentially be able to approximate the actual sampling distribution (Efron & Tibshirani, 1993). The sample output from the Stata statistical package is shown below.

 

Stata statistical package example and result output

use "H:\Document\maths.dta"

reshape long Ques, i(student_id) j(item)

for num 1/10:  gen ThX = -(item==X) 

bs "clogit Ques Th1-Th10, group(student_id)" "_b[Th1] _b[Th2] _b[Th3] _b[Th4] _b[Th5] _b[Th6] _b[Th7] _b[Th8] _b[Th9]",reps(1000) cluster(student_id)

 

Variable	Observed	Bias	Std. Err.	[95% Conf. Interval]
_bs_1	0.708	0.018	0.303	0.113	1.303	(N)
				0.100	1.305	(P)
				0.037	1.260	(BC)
_bs_2	0.747	0.028	0.299	0.159	1.334	(N)
				0.199	1.405	(P)
				0.135	1.335	(BC)
_bs_3	0.670	0.011	0.293	0.094	1.247	(N)
				0.084	1.252	(P)
				0.038	1.230	(BC)
_bs_4	0.952	0.043	0.309	0.345	1.560	(N)
				0.385	1.582	(P)
				0.331	1.472	(BC)
_bs_5	0.597	0.009	0.296	0.015	1.178	(N)
				0.035	1.210	(P)
				0.031	1.174	(BC)
_bs_6	0.526	0.014	0.296	-0.056	1.108	(N)
				-4.51E-16	1.097	(P)
				-0.031	1.090	(BC)
_bs_7	0.491	0.007	0.290	-0.077	1.061	(N)
				-0.066	1.084	(P)
				-0.065	1.080	(BC)
_bs_8	0.561	0.016	0.293	-0.014	1.137	(N)
				1.15E-16	1.122	(P)
				-0.031	1.096	(BC)
_bs_9	0.561	0.011	0.295	-0.016	1.140	(N)
				-0.015	1.166	(P)
				-0.036	1.139	(BC)

Note: N = normal, P = percentile and BC = bias-corrected.

 

R-statistical package example and result output

library(boot) ## bootstrap library is needed

library(splines) ## need this library

library(survival)## need this library

####estimating the full sample

examboth <- read.table('H:\Document/maths.txt', header=T)

combine <- reshape(examboth, v.names="resp", idvar = "id", timevar="item", varying=list(c("Ques1","Ques2","Ques3","Ques4","Ques5","Ques6","Ques7","Ques8","Ques9","Ques10")), direction="long")

indices <- sample(length(combine[,1]), replace=T)

boot.cond <- function(combine, indices, maxit=20){

full.i.dummy <- diag(nlevels(factor(combine$item)))[factor(combine$item),]

full.i.dummy <- 0 - full.i.dummy # turns (0,1) into (0, -1)

full.i.dummy <- data.frame(full.i.dummy, row.names=NULL)

dimnames(full.i.dummy) [[2]] <- paste("i", 2:11, sep="")

attach(full.i.dummy)

examboth.clog <- clogit(resp ~ i2 + i3 + i4 + i5 + i6 + i7 + i8 + i9 + i10 + strata(id), data= combine[indices,])

coeff <-coefficients(examboth.clog)

return(coeff)

}

 

Rasch.boot <- boot(combine, boot.cond, 1000, maxit=100) 

Rasch.boot

 

ORDINARY NONPARAMETRIC BOOTSTRAP

Call:

boot(data = combine, statistic = boot.cond, R = 1000, maxit = 100)

Bootstrap Statistics :

     original     bias    std. error

t1* 0.7084904 -0.7024243   0.2957786

t2* 0.7470233 -0.7412647   0.2929619

t3* 0.6707143 -0.6701935   0.2994406

t4* 0.9527469 -0.9553256   0.2943158

t5* 0.5972723 -0.5869482   0.2862424

t6* 0.5264065 -0.5244834   0.3029250

t7* 0.4918603 -0.4915181   0.3067102

t8* 0.5615339 -0.5602604   0.2915319

t9* 0.5615339 -0.5531485   0.3065304

 

            In the programming output, the tenth item (item 10), with associated beta (1) = 0 is the reference level. This is because; the conditional logit function programming is not able to define a reference level if item 10 is added. The observed and original values in Stata and R-statistical software are the conditional logistic Rasch difficulty parameters.

Discussion

            The purpose of this short communication has been to demonstrate two statistical software methods for estimating the bootstrap application of conditional item difficulty estimates in Rasch to teachers or Rasch users with little programming skills. In recent years, measurement research continues to broaden and the bootstrap application to item difficulty estimates in Rasch becomes a suitable procedures for demonstrating binary items for a very small number of persons which existing Rasch measurement software can not estimate.

References

Baron, J. & Li, Y. (2004). Notes on the use of R for psychology experiments and questionnaires. Available at http://www.psych.upenn.edu/~baron/rpsych/rpsych.html

 

Davidson AC, Hinckley DV (1997). Bootstrap Methods and Their Applications. Cambridge, England: Cambridge University Press.

 

Efron, B. (1979). Bootstrap methods: Another look at the Jackknife. Annals of Statistics, 7, 1-16.

 

Efron, B and Tibshirani, J.C (1993).  An introduction to the bootstrap. New York: Chapman & Hall. 

 

Fisher, G. H. and Molenaar, I.W. (1995). Rasch models. foundations, recent developments and applications. New York: Springer-Verlag.

 

Rasch G. (1960/1980).  Probabilistic models for some intelligence and attainment test. Chicago: University of Chicago Press. (Originally published by The Danish Institute for Educational Research, Copenhagen, 1960).

 

StataCorp. Stata Statistical Software, Release 8.2. In. College Station, TX: Stata Corporation; 2003.

 

Weesie, J. (1999). The Rasch model in STATA.  STATA statistical software 7.0 : STATA Corporation.