Virtual Equating of Items

When two test forms have no respondents in common ("common-person equating") and no items in common ("common-item equating"), then the data for each test form comprises a separate analysis. If the test forms are designed to be parallel, then it may be reasonable to assert that the mean item difficulties of the two test forms are the same. If the distributions of the respondents administered each test forms are considered to be randomly equivalent, then it may be reasonable to assert that the mean respondent abilities are the same. But what if these assertions are unreasonable or need to be verified? Then conduct a qualitatively-based virtual equating (Luppescu, 1996).

Step 1. Identify pairs of items of similar content and difficulty in the two tests. Be generous about interpreting "similar" at this stage.

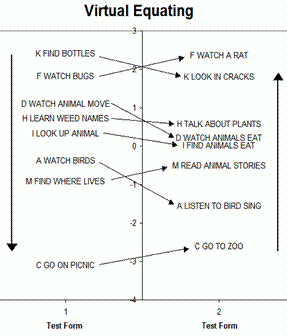
Steps 2-4 by print-out: The two item difficulty hierarchies are printed with the difficulties spaced according to their Rasch measures. Equivalent items are identified. The sheets of paper are moved relative to each other until the overall joint hierarchy makes the most sense. The value on Test A corresponding to the zero on Test B is the equating constant to use for Test B. If the item spacing on one test appears expanded or compressed relative to the other test, then rescale the measures on one test form to compensate.

Or: Step 2 by graphing: From the separate analyses, crossplot the difficulties of the pairs of items, with Test B on the y-axis and Test A on the x-axis. The slope of the best-fit line i.e., the line though the point at the means of the common items and through the (mean ±1 S.D.) point should have slope near 1.0. If it does, then the intercept of the line with the x-axis is the equating constant. To place Test B in the Test A frame of reference: add the x-axis intercept to all Test B measures.

Step 3. Examine the scatterplot. Points far away from the best fit line indicate items that are not good pairs. You may wish to consider these to be no longer paired. Drop the items from the plot and redraw the best fit line.

Step 4. The slope of the best fit is: slope = (S.D. of Test B common items) / (S.D. of Test A common items) . So multiply Test B measures by the value of 1/slope, and add the value of the x-intercept. Then reanalyze Test B. Test B is now in the Test A frame of reference, so a cross plot of the equating items should approximate the identity lined. If so, the person and item measures from Test A and Test B can be reported together.

Luppescu, Stuart (1996). Virtual equating: An approach to reading test equating by concept matching of items. Doctoral dissertation, University of Chicago.

Virtual equating of examinee groups is discussed in "Equating Without an Anchor for Nonequivalent Groups of Examinees", Nicholas T. Longford, Journal of Educational and Behavioral Statistics, June 2015, vol. 40, no. 3, 227-253

Virtual Equating. Luppescu S. … Rasch Measurement Transactions, 2005, 19:3 p. 1025

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt193a.htm

Website: www.rasch.org/rmt/contents.htm