Dichotomous Equivalents to Rating Scales

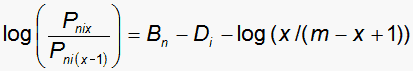
There are numerous ways to conceptualize rating scales. One useful conceptualization is to imagine that the rating scale is equivalent to a set of dichotomous items. Huynh Huynh investigated this: Huynh H. (1994) On equivalence between a partial credit item and a set of independent Rasch binary items. Psychometrika, 59, 111-119, and Huynh H. (1996) Decomposition of a Rasch partial credit item into independent binary and indecomposable trinary items. Psychometrika, 61, 31-39.

A crucial finding is that the Rasch-Andrich thresholds must advance (i.e., not exhibit "threshold disordering") for a polytomy to have the mathematical properties of a set of dichotomies. But merely advancing is not enough.

Consider a polytomy with m+1 ordinally advancing categories. There are m transition points, so this could be conceptualized as m dichotomies. As the Rasch-Andrich thresholds for the polytomy become further apart then the set of dichotomous items would have a wider difficulty range. The boundary condition is that the m dichotomies be of equal difficulty. Then a score of k on the polytomous item would be equivalent to scoring k on m equally-difficulty dichotomies.

A set of equally difficulty dichotomies constitute a set of Bernoulli (binomial) trials. The polytomous Rasch model for this is (with the familiar notation):

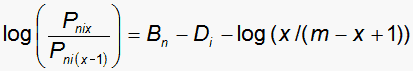This provides the lower limits by which Rasch-Andrich thresholds must advance in order that a polytomy have the same mathematical properties as a set of dichotomies. A useful rule-of-thumb is "thresholds must advance by one-logit". The exact values are tabulated below.

John Michael Linacre

Dichotomous Equivalents to Rating Scales, Linacre J.M. … Rasch Measurement Transactions, 2006, 20:1 p. 1052

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt201d.htm

Website: www.rasch.org/rmt/contents.htm