Rating Scale Equivalence to Dichotomies

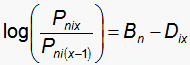
Question: We have 5 dichotomous items based on the same reading text. What would happen if we replace the dichotomies with a rating scale item scored 0-5?

Answer: This is an attractive option if the target dichotomies exhibit more local dependence than the other items on the test. Let us first suppose that the 5 items fit the Rasch model about as well as the other items on the test. Then here is a standard polytomous rating scale model:

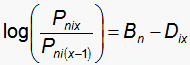and here is an example of one of the five items:

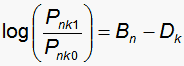Then, for these to be equivalent,

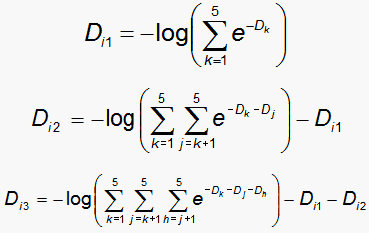and similarly for D_i4, Di_i5. The overall difficulty of a polytomous item is given by

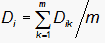giving F_ik = D_i - D_ik as the Rasch-Andrich thresholds.

In general, the overall difficulty of the polytomous item will not match the average difficulty of the equivalent dichotomous items. If the local origin of the measurement scale is set at the average difficulty of the items, it is seen that the local origin will also change location, so that the person measures will change value. But all person measures will change by about the same amount.

Example: Dichotomous item difficulties are {1,2,3,4,5} logits. Then the D_ix are {.55, 1.87, 3.0, 4.13, 5.45} logits.

So what will happen if your 5 items are more locally dependent than the other items on the test? If the local dependence increases their fit to the Rasch model, then they will be more discriminating than 5 independent Rasch dichotomous items. Consequently the {D_ik} will be less dispersed than the values given above.

But if the local dependence is on a secondary dimension, so that it decreases their fit to the Rasch model, then the {D_ik} will be more dispersed than the values given above.

John Michael Linacre

Rating Scale Equivalence to Dichotomies, Linacre J.M. … Rasch Measurement Transactions, 2006, 20:1 p. 1052

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt201e.htm

Website: www.rasch.org/rmt/contents.htm