Item Discrimination and Rasch-Andrich Thresholds Revisited

Linacre (2006) concludes that it might be an advantage to have thresholds reversed relative to their natural order because the expected value curve is then steeper and more discriminating than if the items are in their natural order. He uses the case of four discrete dichotomous items being summed to form a polytomous item with a maximum score of 4 to illustrate his point. This note demonstrates that the apparent improved discrimination in such a case is artificial. It is directly analogous to over discrimination in the case of dichotomous items. This point is explained below.

The Rasch model for more than two ordered categories can be expressed as:

(1)

where

(2)

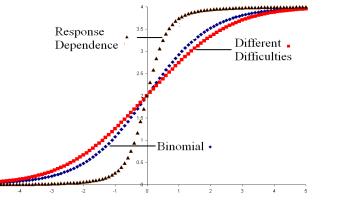
Figure 1: ICCs for three subtests

Suppose we sum the responses of four discrete and statistically independent dichotomous items of equal difficulty and these are analyzed according to Eq. (1) in which . Let us call the item so formed a subtest.

First, because the items have equal difficulty and are statistically independent, the total score of the subtest results in a binomial distribution. In that case the model of Eq. (1) specializes to

and the thresholds take on very specific values. In the case of four items, these values are -1.39, -0.41, 0.41 and 1.39 (Andrich, 1985). Notice that they are symmetrical, as would be expected, and properly ordered. These values have nothing to do with the distribution of persons, or the relative difficulties of the items - they characterize the response structure among scores, given the location of the person and the item.

The two requirements of a binomial distribution, equal difficulty of items and statistical independence, may be violated in two simple ways. First, the items may be of different difficulty, and second, the responses may not be independent. If the items are of different difficulty but independent, then the distribution of scores in the subtest for any and will regress to the central scores and there will be a greater proportion of frequencies in the middle scores than in the binomial. This difference in difficulty will not violate the general Rasch model, however.

Second, if the items are of the same difficulty but there is response dependence among the items, then a score of 1 in one item will give a greater probability of 1 for a dependent item than if there were no dependence, and correspondingly a score of 0 in one item will give a greater probability of 0 in the dependent item than if there were no dependence. Thus if the items are of the same difficulty but the responses are dependent, then the distribution of scores in the subtest for any and will diverge to the extremes scores and there will be a greater proportion of frequencies in the extreme scores than in the binomial. This is opposite to the effect of items having items of different difficulty in the presence of statistical independence.

Table 1 shows the probabilities of each score of a subtest composed of four discrete items under three conditions for the case where . In Case 1 the items are of equal difficulty, and statistically independent and give a binomial distribution, in Case 2 items have different relative difficulties, , but statistical independence holds, and in Case 3 the items are of equal difficulty 0, but all items show statistical dependence on the response of the first item. The dependence is constructed in the following way: for a value of , if the response to item 1 is , then the probability of a response is

i=2,3,4; and if the response on item 1 is , then the probability of a response for subsequent items is

i=2,3,4. That is, if the response to the first item is 1, the probability of a response of 1 for subsequent items is greater than if there was no dependence, and if the response to item 1 is 0, then the probability of a response of 1 is less than if there was no dependence. This may occur in a set of four items all of which belong to one reading stem, and the correct response to the first item gives clues to the correct responses to the other items.

Table 1
Distributions of total scores for the binomial, for items of different difficulties, and for items with responses dependent on the first item

It is clear from Table 1 that when the items are of different difficulty, that the probability of the middle score of 2 in the subtest is greater than in the binomial distribution, and when items 2, 3 and 4 have response dependence on item 1, the probability of extreme score in the subtest is greater than in the binomial. An extreme case of dependence would be where the three items were totally dependent on the first, in which case all responses would be the same, and all scores would be 0 or 4. Table 2 shows the threshold values which correspond to the frequencies shown in Table 1.

Table 2
 Thresholds for the binomial distribution and one with items of different difficulty and one with items with response dependence on the first item

In particular, in the subtest where the items are of different difficulty and the responses are independent, the thresholds are further apart than in the binomial distribution; in the subtest where the items are of the same difficulty but the responses of items 2, 3 and 4 are dependent on the response to item 1, then the thresholds are closer together than the binomial, and even reversed relative to the natural order.

Figure 1 shows the Item Characteristic Curves (ICCs) for these three subtests. It is evident that the slope of the ICC, that is the discrimination, for the subtest with response dependence is the greatest, and that for the subtest with items of different difficulty it is the least. The subtest with a binomial response structure and which provides the frame of reference for the analysis and interpretation., has a slope between the other two subtests.

However, it should be evident that these curves cannot be interpreted simply in terms of the relative discrimination of the items, with the conclusion that the greater the discrimination the better. In particular, the ICC of the subtest with dependence, the information is not equivalent to that from four independent items. Instead the information available from these four items is less than would be obtained from the same number of i statistically independent items. The model for ordered categories follows the data in obtaining the threshold estimates, and accounts for the dependence among the items, but the information available is less than if the items were statistically independent.

Indeed the effect shown here is well known in traditional test theory (TTT). In TTT, the reliability index is a key statistic to evaluate a test. And the greater the correlation among items, the greater the reliability. However, TTT adherents observed that the reliability is the highest when all items are identical, and understood that they then effectively have only one item. In that case the validity of the test was that of just one item. They called this reduction in validity with such an increase in reliability as the attenuation paradox.

The Rasch model, and the above analysis provides an understanding of this paradox, and the binomial distribution provides a criterion to assess if there is dependence among subsets of items. Because differences in item difficulty and dependence in responses have opposite effects on the distribution of total scores of a subtest of each person, the binomial thresholds can be used as a conservative criterion to identify dependence. Specifically, because items will generally have some difference in difficulty, if the thresholds of a subtest are closer together than those of the binomial (or reversed), then it follows that there must be response dependence. If the items have different difficulty, then there must be even more response dependence than if the items are of the same difficulty.

This analysis and specific values for different maximum scores of a subtest that provide a conservative criterion for evidence of dependence is provided in detail in Andrich (1985). The application of the Rasch model in understanding the attenuation paradox of TTT is also described in Andrich (1988). In summary, the dichotomous Rasch model fixes the test discrimination as a kind of average of the discrimination of all items, and under discrimination of any items relative to this average suggests multidimensionality, while over discrimination relative to this average suggests response dependence. This is one basic difference between the perspectives of TTT and a Rasch model analysis. In TTT, the greater the discrimination of an item the better, though there is an awareness that items may over discriminate and not add to the validity of the test; in a Rasch model analysis there is an explicit criterion of over discrimination relative to the test as a whole as an indicator of possible response dependence. The above example in which a subtest is composed of discrete items, shows that the idea of over discrimination in dichotomous items can also manifest itself with a polytomously scored item. In this case the over discrimination in some sense accounts for dependence among the discrete items, but it does not add to the information, instead, in accounting for the dependence it shows that there is less information in the subtest than if the items were independent.

Thus there is a lesson to be learned from the above analysis. The information is in the data, and information cannot be contrived which might show some better index without understanding how the model interacts with the data and how it manifests properties of the data, including properties that are dysfunctional in the data. In our case of four discrete items above, the very high discrimination reflects statistical dependence and less information than if the items were statistically independent. That is, there is no greater information in the data of the subtest just because it has been rearranged and analyzed in a different way resulting in a manifest high discrimination in the subtest. In the extreme case we mentioned above, if the responses to the items were identical reflecting total dependence, all responses would be 0 or 4, and the thresholds would be so reversed that the ICC for the subtest would be vertical at the subtest difficulty. This would give the impression that at this point there is infinite information! Clearly, this is not case - the information is just that of a single item.

David Andrich, Murdoch University

Andrich, D. (1985). A latent trait model for items with response dependencies: Implications for test construction and analysis. Chap. 9 in S. Embretson (Ed.), Test design: Contributions from psychology, education and psychometrics. Academic Press, New York

Andrich, D. (1988). Rasch models for measurement. Sage Publications.

Linacre, J.M. (2006) Item Discrimination and Rasch-Andrich thresholds. Rasch Measurement Transactions, 20, 1, 1054.

Item Discrimination and Rasch-Andrich Thresholds Revisited, Andrich, D.A. … Rasch Measurement Transactions, 2006, 20:2 p. 1055-7

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt202a.htm

Website: www.rasch.org/rmt/contents.htm