Bernoulli Trials, Fisher Information, Shannon Information and Rasch

Jakob Bernoulli (1654-1705) wrote the founding treatise on mathematical probability, Ars Conjectandi, published posthumously in 1713. This discusses binomial trials, known to us as dichotomous items.

Bernoulli explains that, if the probability of passing a dichotomous item is p, this is also the expected value of the trial when a success is scored 1 and a failure 0. After n identical trials, we expect to have n*p successes and n*(1-p) failures. The sum-of-squares of these around their expectation, p, is n*p*(1-p)^2 for the successes and n*(1-p)*(0-p)^2 for the failures. Thus total sum-of-squares

= n*p*(1-p)^2 + n*(1-p)*(0-p)^2 = n*p*(1-p)

so the sum-of-squares for a single trial, its Bernoulli variance, is n*p*(1-p)/n = p*(1-p).

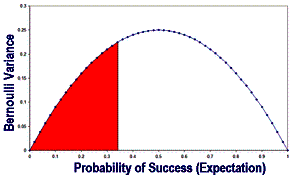
The curve of Bernoulli variance against probability of success is plotted here in Figure 1.

Figure 1. Bernoulli variance of one binomial trial.

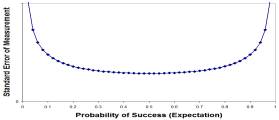
The reciprocal of this curve I = 1 / (p * (1-p) ) is Ronald Fisher's (1925) "statistical information" function for a binomial response, shown in Figure 2. Fisher defined statistical "information" to be the "intrinsic accuracy of the error curve".

Suppose that the probability is a function of a variable, x, so that p = p(x). This function has the property that it is the accumulation (integral) of the Bernoulli variance (indicated by the red area in Figure 1). Then, since the variance is always positive, p(x) always increases as x increases. p(x) increases most rapidly with x when the Bernoulli variance is at its maximum where p=0.5 and p(x) =0.25. What is the function? It must satisfy the integration:

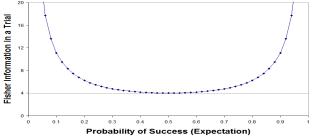
Figure 2. Fisher Information in one binomial trial.

integral( (p(x)*(1-p(x))) dx = p(x)

or, written as a differential equation,

dp(x) / dx = p(x)*(1-p(x))

for which the solution is

p(x) = exp(x) / (1+exp(x))

This is the logistic ogive of the Rasch model, with x being the difference between the person ability and the item difficulty for a dichotomous item. So p(x), the Rasch logistic ogive, has the property that its rate of change, its slope, is the Bernoulli variance, the inverse of the Fisher information.

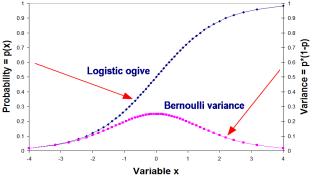
Figure 3. Rasch logistic ogive and Bernoulli variance.

Figure 3 shows the logistic ogive and the Bernoulli variance of Figure 1, now redrawn in terms of the independent variable x, which we can interpret as the Rasch measure-difference. It can be seen that the slope of the logistic ogive curve is given by the variance curve, and that the accumulation of the variance curve is the logistic ogive.

When we re-express the Rasch logistic ogive in terms of p, then we have the log-odds form of the Rasch dichotomous model:

x = log_e (p / (1-p))

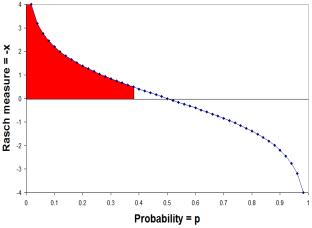
Figure 4. Reoriented Rasch logistic ogive.

Redrawing Figure 3 in terms of p on the x-axis, and -x on the y-axis, we have Figure 4, an ogive with the vertical orientation originally used by Francis Galton (1875), except that he had the tall men stand on the right side, not the left. The area under this curve (shown in red) is an indication of the entropy in the curve. It can be expressed by H where

H = integral (-x)dp = - (p*log_e(p) + (1-p)*log_e(1-p))

This is equivalent to Claude Shannon's (1948) "binary entropy function" which he identifies as related to the communication information in a binary observation, and also to the entropy function in Boltzmann's (1872) statistical mechanics. Shannon expressed his function in terms of log2(p), which is 1.44 * loge(p). Shannon's information function is plotted here in Figure 5. Its maximum value is 1.0.

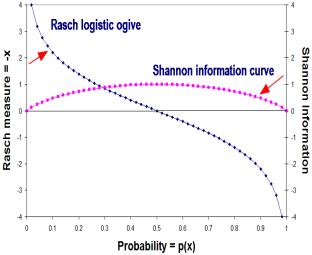
Figure 5. Shannon information and the Rasch ogive.

The Rasch ogive is seen to tie together neatly Fisher information and Shannon information. In the literature, these are presented as contradictory formulations. An example is "... a theory based upon Fisher information [may be] less powerful than one based on Shannon information" (Wikipedia, art. "Physical Information"). In fact, Fisher Information and Shannon Information are different ways of saying the same thing.

John Michael Linacre

Shannon, C. E. (1948). A mathematical theory of communication (parts I and II). Bell System Technical Journal, XXVII:379-423.

Boltzmann L. (1872) Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen, Wiener Berichte, 66: 275 - 370 ("Further studies on heat equilibrium among gas molecules")

Fisher, R. A. (1925). Theory of statistical estimation, Proc. Camb. Phil. Soc., 22: 700-725.

Galton, F. (1875) Statistics by intercomparison, with remarks on the law of frequency of error. Philosophical Magazine, 4th series, 49: 33 - 46.

Bernoulli Trials, Fisher Information, Shannon Information and Rasch, Linacre J.M. … Rasch Measurement Transactions, 2006, 20:3 p. 1062-3

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt203a.htm

Website: www.rasch.org/rmt/contents.htm