DIF matters: A practical approach to test if
Differential Item Functioning makes a difference

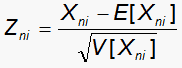
Differential Item Functioning (DIF) in psychometric tests has long been recognized as a potential source of bias in person measurement. Originally called `item bias' (Lord, 1980), the analysis of DIF is concerned with identifying significant differences, across group membership, of the proportion of individuals at the same apparent ability level who answer a given item correctly (or can do a particular task). If an item measures the same ability in the same way across groups then, except for random variations, the same success rate should be found irrespective of the nature of the group. Items that give different success rates for two or more groups, at the same ability level, are said to display DIF (Holland & Wainer, 1993). When developing new tests, items displaying DIF would normally be revised or discarded.

Existing tests may also contain items displaying DIF. Sometimes summary and individual item fit statistics are satisfactory, yet DIF is still apparent. If DIF occurs within a Rasch model framework, it may be productive to treat items exhibiting DIF as different items for different groups. This process is called "splitting for DIF". It produces DIF-free person estimates (Tennant A, et al, 2004), but the data manipulation can be complex and time-consuming (Hambleton 2006).

Another issue is that of "cancellation of DIF" (Teresi JA, 2006). This is where some items favor one group and other items the other group. In practice, DIF always balances out as it is conditional upon the raw score. That is, at a given level of the trait corresponding to an overall score of 'x', we would expect members of a group to have a particular success rate on an item. When this success rate is considerably less due to DIF against the group, then the group's overall success-rate needs to be made up from elsewhere in order for the group members obtain the score of 'x'. The success-rate may be made up from another item which balances the original DIFed item, or the counter-balancing effect may be spread across many items.

Our Study
Although two types of DIF can be identified - uniform DIF (constant across ability levels) and non-uniform DIF (varying across ability levels. In our simulation study, we looked only at Uniform DIF. To do this, we simulated four datasets:

SET A: a 20 item 5 category (0-4) response set with 400 cases, divided evenly between males and females, where two items are simulated to have DIF, both giving males a higher expected score on each item.

SET B: replicated the first set except with 10 items.

SET C: replicated the first set except with just 5 items.

SET D: replicated SET B but with DIF adjusted so that one item favored males, the other item females, both by one logit, i.e., perfect cancellation.

All datasets were simulated to have the same item difficulty range and the same rating scale structure. Item difficulty was modified just for the two items showing DIF in the relevant part of the sample, to represent DIF by gender. These different sets would be typical of many scales (or subscales) used in medical outcome studies.

Approach
Items were first fitted to the Rasch-Masters Partial Credit model with the RUMM2020 program. In our study, DIF is examined through response residuals. When person n encounters item i, the observed response is Xni and the corresponding expected response is E[Xni], with model variance V[Xni]. The standardized residual Zni is given by

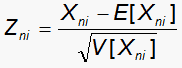(1)

Then each person is assigned to a factor group (e.g., gender) and classified by ability measure on the latent trait into one of G class intervals. Then, for each item, the observation residuals are analyzed with a two-way analysis of variance (ANOVA) or person factor by class interval. The presence of DIF is indicated by statistically significant inter-person-group variance.

Once DIF was identified using ANOVA, the strategy we adopted is a variation of the iterative 'top-down purification' approach, in which the requirement for assessing DIF is a baseline set of 'pure' items (Lord, 1980). In our approach we identified the 'pure' item set by removing items displaying DIF. Given the pure set, the item parameter estimates [= item difficulties + Rasch-Andrich thresholds] for the three items displaying the least DIF (2 items for the Set C 5-item simulation) were exported to an anchor file. The original full set of items was then re-run anchored by those three items so that person estimates were based upon the measurement framework defined by the anchored items which show the minimum DIF. This accords with the measurement framework of the pure analysis. The person estimates from the two analyses (pure and full-with-anchors), plus the standard errors of the estimates, were then exported into Excel and compared.

Irrespective of the amount of DIF detected, we argue that for practical purposes, given satisfactory fit to the model, if the person estimates remain largely unchanged, then the DIF is trivial and can be ignored. We define a trivial impact as being a difference in the person estimates from the two analyzes of less than 0.5 logits (Wright & Panchapakesan, 1969).

A final analysis confirms the unidimensionality of the full data set, to make sure this has not been compromised by DIF. A principal-components analysis of the residuals identifies positive and negative loading subsets of items which are used to generate estimates for comparison using a series of independent t-tests. Where the number of significant individual t-tests does not exceed 5% (or the lower bound of the binomial confidence interval does not) then the scale is unidimensional (Smith, 2002).

Routine summary fit statistics are reported for each simulation, including item-and person mean residuals and their standard deviations, which would be zero and one respectively under perfect fit. A Chi square interaction value reports on invariance across the trait, and would be non-significant where data meet model expectations. A Person Separation Index is also reported, equivalent to Cronbach's Alpha, as a measure of person sample "test" reliability.

Our sample size of 200 per group is sufficient to test for DIF in the residuals where at a of p<0.05, ß of p<0.20 the effect size between groups is 0.281. Bonferroni corrections are applied to both fit and DIF statistics due to the number of tests undertaken for any given scale (Bland & Altman, 1995).

Our Findings
In the analyses of all 4 datasets, the two items simulated to have DIF were reported to have significant DIF, only one other item, in SET C, was reported to have significant DIF. All 4 datasets showed good fit to the Rasch model, and were not rejected by the test of unidimensionality at the 5% level. The crucial results are shown here:

In each simulated dataset, the ANOVA-based DIF analysis detected the simulated uniform-DIF items. Only in SET C did an additional DIF item emerge and this was purely compensatory to the simulated DIF. Although not significant, all items showed some level of DIF, indicating how the presence of two items favoring males forced other items to favor females. This 'cancellation' phenomenon is well known and raises some important issues (Teresi JA, 2006). It has been argued removal of the items with the most severe level of DIF may actually induce more, rather than less, DIF at the test score level.. Thus total test scores can meaningfully be used for the comparison of populations, even though they are made up of items that are individually DIFed (Borsboom,2006).

An example DIF of behavior (for Item 1 of SET B) is shown in Figure 1. This pictures how uniform DIF puts one group to the left (easier) side of the Rasch ICC, and the other group to the right (harder) side.

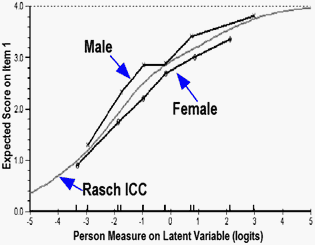Figure 1. DIF on item 1 of the 10 item set (SET B).

SET C raises the DIF content to 40% by reducing the item set to five items. In this dataset, one of the items simulated without DIF demonstrated compensatory DIF, although this disappeared when the two simulated DIF items were removed to obtain the pure set. Compensatory DIF is where one or more items are forced to compensate for primary DIF, as in our two simulated DIF items. However, the extent of cancellation (does it fully compensate?) remains an empirical question. Thus, while all fit statistics showed fit to model expectation, on this occasion, 39.4% of the sample recorded a difference in estimates greater than 0.5 logit.

In SET C, where person estimates differ considerably, the mean difference between males and females increased from 0.18 logits to 0.33 logits in the unDIFed and DIFed item sets respectively. However, the compensatory DIF may lead the analyst to presume that DIF is canceling out, but clearly there is a significant impact on individual estimates, and some impact on group estimates. Thus any analysis where gender (or any other factor) is a substantive component may detect gender differences where they do not exist, simply because of the DIFing effect at the test level (although in this case the difference was non significant). It seems imperative, in the presence of DIF, even with fit to model expectations, to explore the impact on person estimates and see if the DIF makes a difference.

Finally Set D, which included two exactly-canceling items, also showed good fit to model expectations, and both simulated DIF items showed up as significant. The main difference in the results for this set was that the magnitude of difference between estimates was virtually zero for all cases with no cases outside a difference of 0.5 logits (the highest difference was 0.06 logits). In SET B, which has the same number of items, but where two are DIFed in the same direction, 4% of person estimates differed by 0.5 logits or more, so here the DIF is not fully compensated.

The results here suggest that the level of substantive DIF may make a difference at both the individual and group level and thus needs to be recognized and routinely reported. This simple strategy, of comparing the estimates from the full set of items with that from the 'pure' set (the former anchored to the most pure items of the latter) is one way of detecting the impact of DIF.

This simple simulation study has shown that it is possible to examine the impact of DIF in existing scales by looking at the effect upon person estimates. This has shown that these estimates may differ considerably under certain conditions, generally linked to the proportion of DIFed items in the test. While exact cancellation results in no difference for person estimates, compensatory DIF may not fully cancel the DIF, even when significant DIF items emerge as a result.

These findings have important implications particularly for those scales used in routine clinical practice. Some scales have clinical cut points which suggest the need for treatment, and little DIF can be tolerated under these circumstances. Further evidence also needs to be sought for the effect of DIF at the group level as increasingly, in international clinical trials, data are pooled from different countries, and so the scales must be invariant by culture.

Alan Tennant, University of Leeds, UK
Julie F. Pallant, Swinburne University of Technology, Australia

References
Bland JM, Altman DG. (1995). Multiple significance tests: the Bonferroni method. British Medical Journal, 310, 170.
Borsboom D (2006) When Does Measurement Invariance Matter? Medical Care, 44:(11) Suppl 3
Hambleton RK (2006) Good Practices for Identifying Differential Item Functioning. Medical Care 44: (11) Suppl 3.
Holland PW, Wainer H (1993) Differential Item Functioning. Hillsdale. NJ: Lawrence Erlbaum
Lord FM (1980) Applications of Item Response Theory to Practical Testing Problems. Hillsdale NJ: Lawrence Erlbaum Assoc.
Tennant A, Penta M, et al. (2004) Assessing and adjusting for cross cultural validity of impairment and activity limitation scales through Differential Item Functioning within the framework of the Rasch model: the Pro-ESOR project. Medical Care, 42: 37-48
Smith EV (2002) Detecting and evaluation the impact of multidimensionality using item fit statistics and principal component analysis of residuals. Journal of Applied Measurement, 3:205-231.
Teresi JA (2006) Different Approaches to Differential Item Functioning in Health Applications: Advantages, Disadvantages and Some Neglected Topics. Medical Care, 44:S152-S170
Wright, BD, & Panchapakesan, N (1969). A procedure for sample-free item analysis. Educational and Psychological Measurement, (29), 23-48.

DIF matters: A practical approach to test if Differential Item Functioning makes a difference, Tennant, A. & Pallant, J.F. … Rasch Measurement Transactions, 2007, 20:4 p. 1082-84

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt204d.htm

Website: www.rasch.org/rmt/contents.htm