Standard Errors and Reliabilities: Rasch and Raw Score

Question: I was taught that all raw scores on a test have the same raw score standard error, SEM, and this is:
SEM = raw score S.D. * sqrt (1-Reliability).
Why do standard errors for person measures differ?

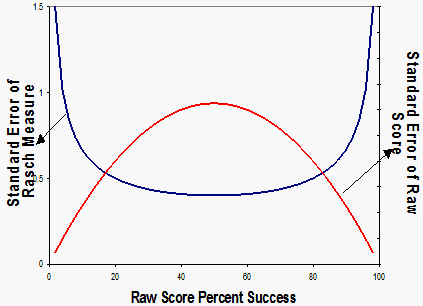
Answer: The raw score "test" reliability (Cronbach Alpha, KR-20, etc.) is based on an average standard error of the raw scores for the sample. Each different raw score on the same set of items has a different standard error. The raw score standard errors are biggest at the center of the test and smallest (zero) at the extreme maximum and minimum scores. Using Bernoulli theory, CTT could compute a standard error for each different raw score, but no one bothers. In contrast, the standard error of a Rasch measure is smallest in the center of the test and biggest at the extremes. Zero and perfect raw scores have raw score standard errors of zero, but the corresponding Rasch measures have infinite standard errors. Since infinity is an impractical number, infinity is usually replaced by the standard error for a conceptual raw score slightly more central by 0.3 score-points, or so, than the maximum or minimum possible raw score.

The plot showns the relationship between the raw score S.E. and the Rasch measure S.E. for a 30 item dichotomous test. The shape of the raw-score S.E. curve can be confirmed by computing the square-root of the binomial variance of each raw score, assuming that the 30 items are equally difficult:

S.E. of measurement of raw score n, corresponding to person ability estimate θ, where L is the number of equally difficult dichotomous items in the test. (If the item difficulties vary, then the following logic is the same, but the arithmetic is a little more difficult.)
Probability of success on one equally-difficult item, P = n/L
Binomial variance of response to 1 item = P*(1-P)
Binomial variance of L items = L*P*(1-P) = Test information at score n or ability θ
Classical Test Theory (CTT) SEM for raw score n = √( L*P*(1-P) ) = √( n * (L-n) / L)
Rasch measure SEM for ability estimate θ corresponding to raw score n = 1 / √( L*P*(1-P) ) = 1 / √( n * (L-n) / L)

Notice that SEM(Raw Score n) ≈ 1 / ( SEM(Rasch Measure θ in logits) )
and
SEM(Rasch Measure θ in logits) ≈ 1 / ( SEM(Raw Score n) )

Classical Test Theory (CTT) computes a "test" reliability = R. From this, an average SEM (standard error of measurement) of the raw scores can be estimated:
Average raw-score SEM = √(1-R) * (observed raw score S.D.).

Rasch computes an S.E. = SEM for each measure. But, like the raw score reliability, the Rasch reliability is also based on the average of the standard errors of the sample ability estimates, θs.

Standard Errors and Reliabilities: Rasch and Raw Score, Rasch Measurement Transactions, 2007, 20:4 p. 1086

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt204f.htm

Website: www.rasch.org/rmt/contents.htm