
There has been a great deal of work done on how to evaluate standard-setting procedures. Hambleton and Pitoniak (2006) suggested procedural, internal, and external criteria for evaluating standard-setting methods. Procedural criteria focus on implementation issues and documentation, internal criteria stress inter-panelist and intra-panelist consistency, and external criteria address comparisons to other methods and the reasonableness of the performance levels.
The two most popular methods for collecting judgments from standard-setting panelists are modified-Angoff and the bookmark procedure (Cizek and Bunch, 2007). The IRT-based bookmark procedure (Mitzel, Lewis, Patz, and Green, 2001 and Lewis, Mitzel, Green, 1996) is becoming the standard-setting method of choice in many statewide assessment programs, even though there has been less research conducted on bookmark methods as compared to modified-Angoff methods (Plake, 2007).
In a series of articles with my colleagues, I proposed using Rasch measurement theory to evaluate the quality of judgments obtained from standard-setting panelists (Engelhard & Anderson, 1998, Engelhard & Cramer 1997, Engelhard & Gordon, 2000, Engelhard & Stone, 1998). A summary of this approach is forthcoming (Engelhard, in press). This approach is based on the many-faceted Rasch (MFRM) model, and it incorporates many of the internal criteria described by Hambleton and Pitioniak (2006). The MFRM model can be used to evaluate the quality of standard-setting judgments obtained from bookmark panelists. The MFRM model for bookmark judgments is:
Loge [Pnijk / Pnij(k-1)] = bn - di - wj - tk [1]
where
Pnijk = probability of panelist n giving a bookmark
rating of k on item i for round j,
Pnij(k-1) = probability of panelist n giving a bookmark
rating of k-1 on item i for round j,
bn = judged performance level for panelist n,
di = judged difficulty for item i,
wj = judged performance level for round j, and
tk = judged performance standard for bookmark rating
category k relative to category k-1. The rating category
coefficients, tk, defines the performance standards or cut
scores.
 |
In order to illustrate the MFR model, an example from Ferdous and Plake (2007) is presented in Table 1. There are six panelists providing bookmark ratings (performance levels from 1 to 4) for five items. The cell entries represent panelist judgments regarding the performance level of each item. The observed means for the items range from 1.00 to 3.67 reflecting the ordered items that would be listed in the ordered item booklet. The observed judgments range from 1.60 to 2.80 with Panelists 2 and 5 having the lowest view of performance and Panelist 4 with the most severe judgments of performance needed to succeed on these five items. This ordering is reflected in the estimated values for the b's and the d's.
 |
This information is presented in the variable map in Figure 1. Both panelists and items are centered at zero, and round (only one round in the example) is not centered. The panelists range in interjudge agreement from 40.0% to 56.0%. The overall observed agreement is 48.0% with an expected agreement of 39.6% based on the model. Item 1 is not included in the agreement statistics because all of the panelists agreed to rate it in category 1.
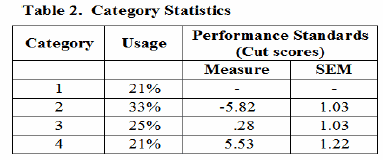 |
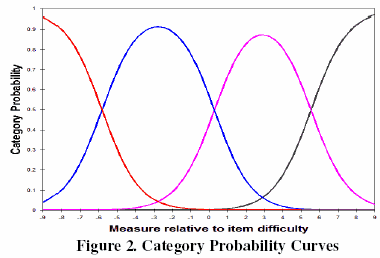
Table 2 presents the category statistics. Within the framework described here, the measures for the category coefficients are defined as the performance standards or cut scores. This definition provides the opportunity to use several graphical displays for practitioners to understand panelist judgments. Figure 2 shows the category probability curves.
 |
Ferdous and Plake (2007) report an interjudge inconsistency index of 36%. If we report this as a consistency or agreement index, then the value is 64%. This value is higher than the Rasch estimate of 48.0% because Item 1 is included in their estimates of interjudge consistency. The MFR model provides the opportunity to go beyond a single index of inter-judge consistency. It also makes available an array of model-data fit indices and graphical displays for exploring more deeply judgments of panelists using the bookmark procedure. Additional work is currently underway to explore the utility of this approach for evaluating bookmark ratings in a variety of standard-setting situations. Experience is still needed to determine whether or not the MFR model can provide a suite of internal criteria for examining bookmark judgments obtained from standard-setting panelists.
George Engelhard, Jr.
Emory University
Cizek, G.J., & Bunch, M.B. (2007). Standard setting: A guide to establishing and evaluating performance standards on tests. Thousand Oaks, CA: Sage
Engelhard, G. (in press). Evaluating the judgments of standard-setting panelists using Rasch measurement theory. In E. V. Smith, Jr., and G. E. Stone (Eds.), Applications of Rasch measurement in criterionreferenced testing, JAM Press.
Engelhard, G., & Anderson, D.W. (1998). A binomial trials model for examining the ratings of standard-setting judges. Applied Measurement in Educ., 11(3), 209-230.
Engelhard, G., & Cramer, S. (1997). Using Rasch Measurement to evaluate the ratings of standard-setting judges. In M. Wilson, G. Engelhard, & K. Draney. (Eds.). Objective Measurement: Theory into Practice, Volume 4 (pp. 97-112). Norwood, NJ: Ablex.
Engelhard, G., & Gordon, B. (2000). Setting and evaluating performance standards for high stakes writing assessments. In M. Wilson & G. Engelhard (Eds.), Objective Measurement: Theory into Practice, Volume 5 (pp. 3-14). Stamford, CT: Ablex.
Engelhard, G., & Stone, G.E. (1998). Evaluating the quality of ratings obtained from standard-setting judges. Educ. and Psychological Measurement, 58(2), 179-196.
Ferdous, A., & Plake, B. (2007). Interjudge inconsistency index for body of work, yes/no, and bookmark standard setting procedures. Retrieved September 2, 2007: www.unl.edu/buros/biaco/pdf/pres07ferdous01.pdf
Hambleton, R C., & Pitoniak, M.J. Setting performance standards. In R. Brennan (Ed.), Educational Measurement, 4th Ed. (pp. 433-470) Westport, CT: Praeger Publishers.
Lewis D.M., Mitzel, H. C., Green, D. R. (1996). Standard Setting: A Bookmark Approach. In D. R. Green (Chair), IRT-Based Standard-Setting Procedures Utilizing Behavioral Anchoring. Symposium presented at the 1996 Council of Chief State School Officers 1996 National Conference on Large Scale Assessment, Phoenix, AZ.
Mitzel, H.C., Lewis, D.M., Patz, R.J., & Green, D.R. (2001). The bookmark procedure: Psychological perspectives. In G.J. Cizek (Ed), Setting performance standards: Concepts, methods and perspectives (pp. 249- 281). Mahwah, NJ: Lawrence Erlbaum Assoc.
Plake, B.S. (2007, April). Standard setters: Stand up and take a stand! 2006 career award address presented at the annual NCME meeting, Chicago, IL.
Evaluating Bookmark Judgements. George Engelhard, Jr. … Rasch Measurement Transactions, 2007, 21:2 p. 1097-1098
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt212a.htm
Website: www.rasch.org/rmt/contents.htm