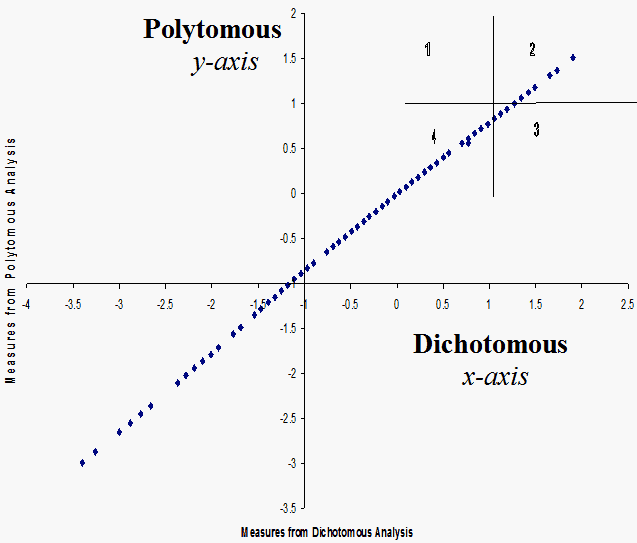
Figure: Plot of person measures from the two analyses. The "+" indicates a hypothetical cut-off score.
Local independence of items is an assumption in Rasch model and all IRT models. That is, the items in a test should not be related to each other. Sharing a common passage, which is prevalent in reading comprehension tests and cloze tests can be a potential source of local item dependence (LID). It is argued in the literature that LID results in biased parameter estimation and affects the unidimensionality of the test. In this study the effects of the violation of the local independence assumption on the person measures are studied.
The items that are put to Rasch analysis are required to be independent of each other. That is, a correct or wrong reply to one item should not lead to a correct or wrong reply to another item. This means that there should not be any correlation between two items after the effect of the underlying trait is conditioned out, i.e., the correlation of residuals should be zero. The items should only be correlated through the latent trait that the test is measuring (Lord and Novick, 1968). If there are significant correlations among the items after the contribution of the latent trait is removed, i.e., among the residuals, then the items are locally dependent or there is a subsidiary dimension in the measurement which is not accounted for by the main Rasch dimension (Lee, 2004). In other words, performance on the items depends to some extent on a trait other than the Rasch dimension which is a violation of the assumptions of local independence and unidimensionality. If the assumption of local item independence is violated, any statistical analysis based on it would be misleading. Specifically, estimates of the latent variables and item parameters will generally be biased because of model misspecification, which in turn leads to incorrect decisions on subsequent statistical analysis, such as testing group differences and correlations between latent variables. In addition, it is not clear what constructs the item responses reflect, and consequently, it is not clear how to combine those responses into a single test score, whether IRT is being used or not (Wang et al., 2005, p.6).
[However, there is always some degree of local dependence in empirical data. So the question becomes: "Does it matter?" One way to answer this is to ask ourselves, "What is the impact of local dependence in these data?" Usually the impact of local dependence is to make the data slightly too predictable, i.e., Guttman-like. The practical impact is to spread the Rasch measures slightly more than they would be if the data were locally independent. Local dependence does not usually impact the ordering of the measures, only their spacing. Accordingly, any statistical tests based on differences between these Rasch measures should be interpreted conservatively, so that differences between measures need to be slightly larger than, say, a t-test would ordinarily require in order to be declared "significant".]
When a set of items are locally dependent they can be bundled into polytomous super-items, that is, the set of items which are related to a common stimulus are considered as one polytomous item to partial out the influence of local item dependence (LID) among items within each super-item. Polytomous Rasch models or IRT models such as Andrich's rating scale model or Masters' partial credit model, etc. are then applied to analyze the testlets. The drawback to bundling dichotomies into polytomies is a loss of statistical and diagnostic information.
The problem of LID is not new and has also been addressed in the classical test theory. Dependency among items can inflate reliability and give a false impression of the precision and quality of the test. It is argued in the literature that if the local independence assumption does not hold, the local dependence itself acts as a dimension. If the effect of LID is substantial it is difficult to say what dimension the main Rasch dimension is. Even if the effect is small, the derived measures will be contaminated, i.e., the measures partially reflect the LID dimension to the extent that LID exists. In fact, LID is a form of violating the unidimensionality principle. LID also results in artificially small standard errors of estimates (SEE) and the overestimation of reliability.

Figure: Plot of person measures from the two analyses. The "+" indicates a hypothetical cut-off score. |
Case Study
In this section the effects of the violation of the assumption of local item independence on the person ability measures in a C-Test are investigated and the impact of LID on decision-making in a hypothetical assessment is studied.
A four-passage C-Test, each passage containing twenty-five blanks, was administered to 160 persons. The C-Test is a variation of the cloze test where the second half of every second word is deleted. Test-takers have to reconstruct the broken words. The C-Test was chosen to conduct this study because the format of the C-Test should be conducive to local dependency and the level of local dependency is presumably high in the context of a C-Test. The data were analyzed twice, once using Rasch's (1960) dichotomous model, treating each gap as an independent dichotomous item and once treating each passage as a polytomous item or testlet (with 25 categories) using Master's (1982) partial credit model. For each person two measures were obtained, one based on the dichotomous analysis and one based on the polytomous analysis.
The measures from the two analyses are cross-plotted in the Figure. The range of the ability measures is wider for the dichotomous measures (5.3 logits) than the polytomous measures (4.5 logits).
As far as criterion-referenced decision-making is concerned we do make somewhat different decisions depending on which analysis we use. In the Figure, a hypothetical cut-score at +1 logit is imposed. For persons who fall in areas 2 and 4 we will be making the same decisions. Test-takers who fall in areas 1 and 3 would have opposite decisions depending on the analysis. Here, no one falls in area 1 but four test-takers fall in area 3. That is, if we base our decision-making on the dichotomous analysis these four people pass and if we decide on the basis of polytomous analysis these four test-takers fail. Depending on the manner in which the +1 logit cut-score was determined, four people may be mistakenly passed or failed depending on the analytical approach.
Conclusion
When the data are expressed in dichotomous form, the local dependence makes the data too predictable. The practical effect is to increase the range of the measures. When the data are summarized into polytomous items, the local dependence is lessened, so making the data less predictable and the range of the abilities narrower.
In the case study, the relationship between the two sets of ability measures is almost linear. Consequently, when the ability measures are rescaled into a more convenient unit for communication to stake-holders, the logit-differences due to local dependence may vanish. Nevertheless, the artificially high reliability and the impact on examinees near a cut-score remain.
Purya Baghaei
Lee, Y. (2004) Examining passage-related local item dependence (LID) and measurement construct using Q3 statistics in an EFL reading comprehension test. Language Testing, 21:1, 74-100.
Lord, F. M. and Novick, M. R. (1968) Statistical theories of mental test scores. Reading, Mass.: Addison-Wesley.
Wang, W. & Wilson, M. (2005) Exploring local item dependence using a random-effects facet model. Applied Psychological Measurement, 29: 4, 296-318.
Local Dependency and Rasch Measures. … P. Baghaei, Rasch Measurement Transactions, 2008, 21:3 p. 1105-6
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Apr. 21 - 22, 2025, Mon.-Tue. | International Objective Measurement Workshop (IOMW) - Boulder, CO, www.iomw.net |
| Jan. 17 - Feb. 21, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Feb. - June, 2025 | On-line course: Introduction to Classical Test and Rasch Measurement Theories (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| Feb. - June, 2025 | On-line course: Advanced Course in Rasch Measurement Theory (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| May 16 - June 20, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 20 - July 18, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Facets), www.statistics.com |
| July 21 - 23, 2025, Mon.-Wed. | Pacific Rim Objective Measurement Symposium (PROMS) 2025, www.proms2025.com |
| Oct. 3 - Nov. 7, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt213b.htm
Website: www.rasch.org/rmt/contents.htm