Assessing Psychiatric Patient Self-Awareness Behavior with Many-Facet Rasch Analysis

The Many-Facet Rasch Model (MFRM) has the great advantage for clinical practice that it allows the practitioner not only to examine and assess the patient behavior patterns, but also to analyze the patient behavior on different occasions. In this study, building on previous research (e. g. Rangell, 1981; Markova & Berrios, 1995) and on psychiatric practice, the Psychiatric Patient Self-Awareness (PPSA) behavior is identified through five self-awareness indexes, namely: 1. Request (the patient decides autonomously to ask for help); 2. Autonomy (the patient is aware of his health status); 3. Content (the reasons why a request for help is advanced); 4. Relations (the patient is able to communicate with the others); 5. Context (the patient is aware of the context where he is acting).

The patients are 48 Italian adult females, mean age 50.29; their school levels are low (65%), medium (30%) and high (5%) . All patients are evaluated by a team of experts (psychiatrists and psychologists) at two successive occasions (time 1: the medical team visits the patient at his/her arrival at the medical center; time 2: the patient is revisited after a period of time which can vary from 20 days to 88 days). At each time-point, the experts rate each patient on the five indexes using a self-awareness rating scale.

There are three facets in the model: 1. patient (48), 2. time-point (2) and 3. index (5). The analysis produced patient measures, index calibration measures on a hypothesized PPSA behavior variable, and time-point measures. The infit statistics and the outfit statistics are satisfactory for time-points, also for the index measures, except for index 1 (request) for which the mean-square fit statistics are slightly above the upper criterion of 1.30 (RMT 8:3, 370 - www.rasch.org/rmt/rmt83b.htm). The majority of the patient measures fit statistics are also satisfactory.

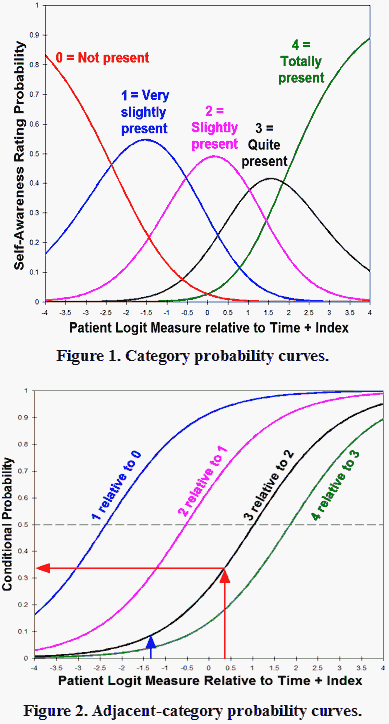
Figure 1 shows the category probability curves for the self-awareness rating scale (0 = not present, 1 = very slightly present, 2 = slightly present, 3 = quite present, 4 = totally present) according to the Andrich rating-scale model. These curves indicate that the experts were able to discriminate the category hierarchy. Figure 2 shows the category relationships, but depicted as the probabilities of the higher ratings in each pair of adjacent categories of the rating scale. These have the form of the familiar Rasch dichotomous logistic ogives. The pairwise ogives have probability 0.5 at the Rasch-Andrich thresholds, where the adjacent categories are equally probable.

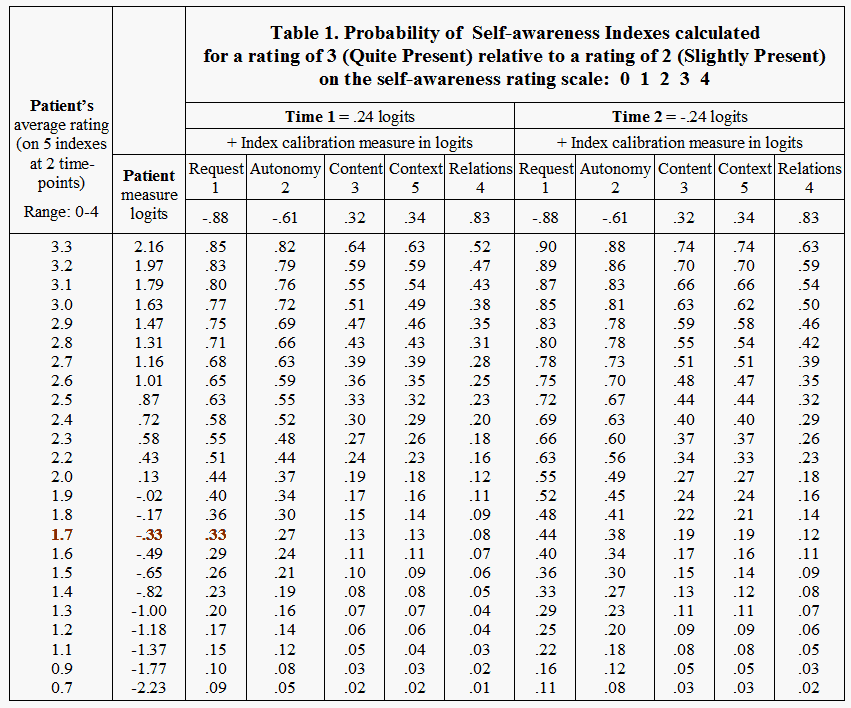
The Table shows the five index measures, the mean raw ratings received by the patients on the Likert scale, the corresponding patient measures and the time measures. Each cell contains the probability of presenting an index which is rated 3 by the experts, relative to a rating of 2, given the index's calibration on the PPSA variable, the overall measure for the patient and the relevant time-point measure.

Table 1, based on Figure 2, is a useful tool for psychiatric assessment of PPSA behavior. Suppose that at time 1 (0.24 logits), a patient with an overall self-awareness mean rating of 1.7 (patient measure = -.33), is rated on index 1 (-0.88 logits) in category 3 ("quite present") . Then the combined measure is -.33 - (0.24 + -0.88) = 0.31. This corresponds to a pairwise probability of 0.33 (arrows in plot, and bold cells in Table). This rating of the index has to be considered quite usual because its relative probability of occurrence on the PPSA variable is rather high (p = .33). But the same cannot be said when a patient rated 3 on index 4 (i.e. the patient is able to communicate with the others) because this has a low probability (p = .08) at a mean score of 1.7 (-1.4 logits in Figure 2).

At time-point 2, the probability of a higher relative rating is always higher than at time 1 in accordance with the difference between the time-point measures, 0.48 logits.

The combination of Rasch analysis and expert clinical knowledge allows us to predict clinical diagnosis of PPSA behavior. Further the inclusion of a time-point facet enables us to investigate and diagnose patient behavior longitudinally, which is helpful in patient treatment and predicting the usage of clinical resources.

Stefania Mannarini

University of Padova - Dept of General Psychology

Renato Lalli

Casa di Cura Parco dei Tigli-Teolo (Pd)

Markova, I.S. & Berrios G.E. (1995). Insight in clinical psychiatry. A new model. The Journal of Nervous and Mental Disease, 183, 12, 743-751.

Rangell, L. (1981). From Insight to Change. Journal of American Psychoanalytic Association, 29, 119-141.

Assessing Psychiatric Patient Self-Awareness Behavior with Many-Facet Rasch Analysis … S. Mannarini & R. Lalli, Rasch Measurement Transactions, 2008, 21:4 p. 1140-1

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt214f.htm

Website: www.rasch.org/rmt/contents.htm