The Rasch Model as a Construct Validation Tool

The definition of validity has undergone many changes. Kelley (1927:14) defined validity as the extent to which a test measures what it purports to measure. Guilford (1946: 429) argued that "a test is valid for any thing with which it correlates". In 1955, Cronbach and Meehl wrote the classic article, Construct Validity in Psychological Tests, where they divided test validity into four types: predictive, concurrent, content and construct, this last one being the most important one. Predictive and concurrent validity were also referred to as criterion-related validity.

Threats to construct validity

One important aspect of construct validity is the trustworthiness of score meaning and its interpretation. The scientific inquiry aiming at establishing this aspect of validity is called the evidential basis of test validity.

A major threat to construct validity that obscures score meaning and its interpretation, according to Messick (1989), is construct under-representation. This refers to the imperfectness of tests in accessing all features of the construct. Whenever we embark on developing a test, we glean some features of the construct according to our definition of the construct (which itself might be faulty and poorly defined) which we plan to measure. And it is very probable that we leave out some important features that we should have included. This narrows the test in terms of the focal construct, and limits the score meaning and interpretation. Messick argues that "the breadth of content specifications for a test should reflect the breadth of the construct invoked in score interpretation" (p.35). The issue has been referred to as authenticity by Messick. "The major measurement concern of authenticity is that nothing important be left out of the assessment of the focal construct" (Messick 1996: 243).

Another threat to construct validity is referred to as construct-irrelevant variance by Messick. There are always some unrelated sub-dimensions that creep into measurement and contaminate it. These sub-dimensions are irrelevant to the focal construct and in fact we do not want to measure them, but their inclusion in the measurement is inevitable. They produce reliable (reproducible) variance in test scores, but it is irrelevant to the construct. Construct irrelevant variance may arise in two forms: construct-irrelevant easiness and construct-irrelevant difficulty. As the terms imply, construct-irrelevant difficulty means inclusion of some tasks that make the construct difficult and results in invalidly low scores for some people. Construct-irrelevant easiness, on the other hand, lessens the difficulty of the test. For instance, construct-irrelevant easy items include items that are susceptible to 'test-wise' solutions, so giving an advantage to 'test-wise' examinees who obtain scores which are invalidly high for them (Messick, 1989).

Rasch measurement issues

The items which do not fit the Rasch model are instances of multidimensionality and candidates for modification, discard or indications that our construct theory needs amending. The items that fit are likely to be measuring the single dimension intended by the construct theory.

One of the advantages of the Rasch model is that it builds a hypothetical unidimensional line along which items and persons are located according to their difficulty and ability measures. The items that fall close enough to the hypothetical line contribute to the measurement of the single dimension defined in the construct theory. Those that fall far from it are measuring another dimension which is irrelevant to the main Rasch dimension. Long distances between the items on the line indicate that there are big differences between item difficulties so people who fall in ability close to this part of the line are not as precisely measured by means of the test. It is argued here that misfitting items are indications of construct-irrelevant variance and gaps along the unidimensional continuum are indications of construct under-representation.

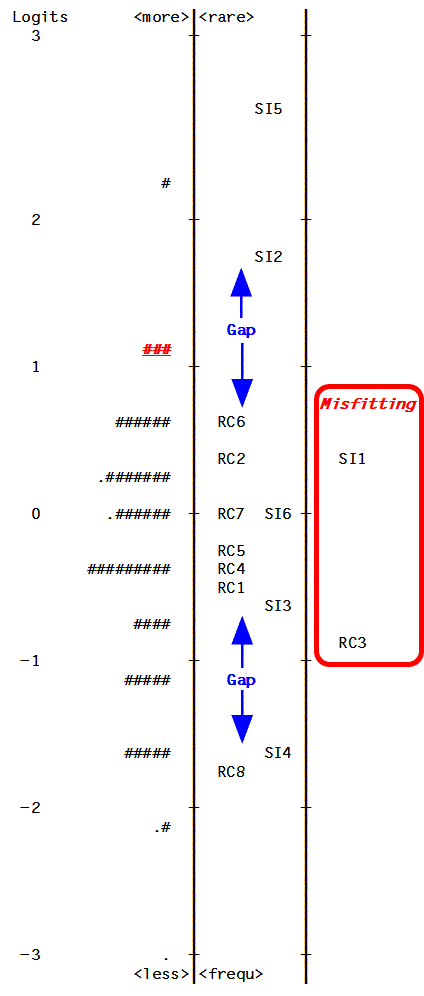
Figure 1 shows a hypothetical unidimensional variable that is intended to be measured with an educational test. The items have been written to operationalize a hypothetical construct according to our construct theory and its definition. The items are coded RC1-RC8 and SI1-SI6. The '#' indicates persons. As you can see, the items and persons are located along one line. The items at the top of the line are more difficult; the persons at the top of the line are more able. As you go down the line, the items become easier and the persons become less able. The vertical line on the right hand side indicates the statistical boundary for a fitting item. The items that fall to the right of this line introduce subsidiary dimensions and unlike the other items do not contribute to the definition of the intended variable. They need to be studied, modified or discarded. They can also give valuable information about our construct theory which may cause us to amend it.

Here there are two items which fall to the right of this line, i.e. they do not fit; this is an instance of construct-irrelevant variance. This line is like a ruler with the items as points of calibration. The bulk of the items and the persons are opposite each other, which means that the test is well-targeted for the sample. However, the distance between the three most difficult items is large. If we want to have a more precise estimate of the persons who fall in this region of ability we need to have more items in this area. The same is true about the three easiest items. This is an instance of construct under-representation.

The six people indicated by ### (each # represents 2 persons), whose ability measures are slightly above 1 on the map, are measured somewhat less precisely. Their ability is above the difficulty of all the items but SI2 and SI5. This means that 12 items are too easy and 2 items are too hard for them. Therefore, they appear to be of the same ability. However, had we included more items in this region of difficulty to cover gap between RC6 and SI2, we would have got a more precise estimate of their ability and we could have located them more precisely on the ability scale. They may not be of the same ability level, although this is what the current test shows. For uniformly precise measurement, the difficulty of the items should match the ability of the persons and the items should be reasonably spaced, i.e., there should not be huge gaps between the items on the map.

The principles of the Rasch model are related to the Messickian construct-validity issues. Rasch fit statistics are indications of construct irrelevant variance and gaps on Rasch item-person map are indications of construct under-representation. Rasch analysis is a powerful tool for evaluating construct validity.

Purya Baghaei, Azad University, Mashad, Iran.

Cronbach, L. J. & Meehl, P. E. (1955). Construct validity in psychological tests. Psychological Bull., 52, 281-302

Guilford, J.P. (1946). New standards for test evaluation. Educational and Psychological Measurement, 6, 427-439.

Kelley T.L. (1927). Interpretation of educational measurements. Yonkers, NY, World Book Company.

Messick, S. (1989). Validity. In R. Linn (Ed.), Educational measurement, (3rd ed.). Washington, D.C.: American Council on Education.

Messick, S. (1996). Validity and washback in language testing. Language Testing 13 (3): 241-256.

Figure 1.

The Rasch Model as a Construct Validation Tool. Baghaei P. … Rasch Measurement Transactions, 2008, 22:1 p. 1145-6

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt221a.htm

Website: www.rasch.org/rmt/contents.htm