Tuneable Goodness-of-Fit Statistics

One of the persistent problems in psychometrics is the determination of the goodness-of-fit between observed and expected values. The problem is particularly tricky with discrete multivariate data that form the basis for measurement in the social, behavioral, and health sciences.

Early work in statistics led to Pearson's chi-square statistic (Pearson, 1900). The chi-square statistic has been quite robust and useful in a variety of applications. Several researchers have proposed adaptations and improvements of chi-square statistics that have ranged from adjustments in the degrees of freedom (Fisher, 1924) to the development of the closely related log_e likelihood ratio statistic (Wilks, 1935). Unfortunately, the assumptions of the Pearson chi-square statistic are not always met, and therefore the χ² sampling distribution is not necessarily a useful guide for judgments regarding model-data fit.

The purpose of this note is to describe a family of tuneable goodness-of-fit statistics based on the Power Divergence (PD) Statistics (Cressie & Read, 1988). Tuneable goodness-of-fit statistics offer a useful approach for examining both person and item fit that has not been explored with Rasch measurement models.

The basic equation for tuneable statistics, τ², is

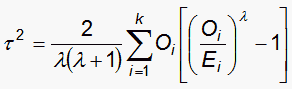where Oi is the observed frequency in a cell i, Ei is the expected frequency for cell i based on the model, and k is the number of cells. Tuneable goodness-of-fit statistics can be obtained by inserting the appropriate λ value. The λ values can range from -∞ to +∞.

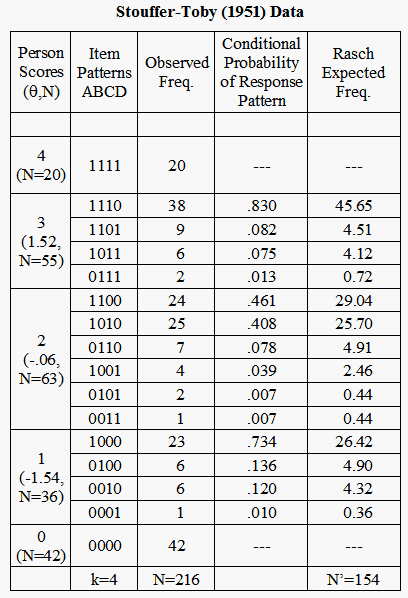
In order to illustrate the use of tuneable statistics, data from Stouffer and Toby (1951) are presented in Table 1. These data are used to illustrate the obtained estimates of τ² for several λ values. See Engelhard (2008) for additional details regarding the Stouffer-Toby scale, as well as the calculation of conditional probabilities and expected frequencies based on Rasch analyses.

Table 1. Stouffer-Toby (1951) Data

Note. Rasch item difficulties are -1.89, -.20, -.10, and 2.20 logits for items A to D respectively.

Conditional probabilities and expected frequencies are based on the Rasch model.

Table 2. Values of the Tuneable Goodness-of-fit statistics

Table 2 presents the values for various goodness-of-fit statistics with λ values reported at various points between -3.00 and 3.00. Some of these λ values correspond to other goodness-of-fit statistics, and these are labeled in the Table 2. The 95th percentile of the chi-squared distribution with 17 degrees of freedom is χ² (17, p=.05) = 27.59. Based on this value, we conclude that the goodness-of-fit is quite good between the observed and expected frequencies based on the Rasch model. Only one of the estimated values suggests rejecting the null hypothesis (λ value = 2).

This note describes a potentially useful set of tuneable goodness-of-fit statistics. It is important to recognize that explorations of goodness-of-fit should not involve a simple decision (e.g., reject the null hypothesis), but also require judgments and "cognitive evaluations of propositions" (Rozeboom, 1960, p. 427).

Additional research is needed on the utility of these tuneable statistics for making judgments regarding overall goodness-of-fit, item and person fit, and various approaches for defining and conducting residual analyses within the framework of Rasch measurement. This research should include research on the sampling distributions for various tuneable statistics applied to different aspects of goodness-of-fit, research on appropriate degrees of freedom, and research on the versions of the τ² statistic that yield the most relevant substantive interpretations within the context of Rasch measurement theory and the construct being measured.

George Engelhard, Jr.

Emory University

Engelhard, G. (2008). Historical perspectives on invariant measurement: Guttman, Rasch, and Mokken. Measurement: Interdisciplinary Research and Perspectives (6), 1-35.

Fisher, R.A. (1924). The conditions under which χ² measures the discrepancy between observations and hypothesis. Journal of the Royal Statistical Society, 87, 442-450.

Freeman, D.H., & Tukey, J.W. (1950). Transformations related to the angular and the square root. Annals of Mathematical Statistics, 21, 607-611.

Kullback, S. (1959). Information theory and statistics. New York: John Wiley.

Neyman, J. (1949). Contribution to the theory of the χ² test. Proceedings of the First Berkeley Symposium on Mathematical statistics and Probability, 239-273.

Pearson, K. (1900). On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philosophy Magazine, 50, 157-172.

Read, T.R.C., & Cressie, N.A.C. (1988). Goodness-of-fit for discrete multivariate data. New York: Springer-Verlag.

Rozeboom, W.W. (1960). The fallacy of the null-hypothesis significance test. Psychological Bulletin, 57, 416-428.

Stouffer, S.A. & Toby, J. (1951). Role conflict and personality. The American Journal of Sociology, 56, 395-406.

Wilks, S.S. (1935). The likelihood test of independence in contingency tables. Annals of Mathematical Statistics, 6, 190-196.

Tuneable Goodness-of-Fit Statistics. Engelhard, G. Jr. … Rasch Measurement Transactions, 2008, 22:1 p. 1158-9

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt221l.htm

Website: www.rasch.org/rmt/contents.htm