Conceptualizing Overfit or Over-parameterization

Students stumble over the meaning of "overfit", indicated in Rasch program output by negative t-statistics and mean-squares less than 1.0 (chi-squares less than their d.f.). This is an aspect of Rasch measurement which sounds strange to analysts familiar with conventional descriptive statistics and model-building.

The nearest thing to overfit in conventional statistical analysis (which fits models to data) is over-parameterization. But statistics courses usually spend little time discussing this problem, so the students imagine that "the better the fit, the better the model!" In building statistical models, they may be instructed to choose between better and worse fitting models, but they are rarely told to reject a model because its fit is "too good".

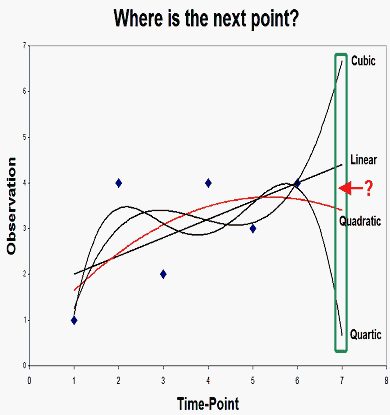
A demonstration of over-parameterization is to put some points on an x-y plot, then fit a series of polynomials with more and more terms to those points. It becomes obvious that too many terms actually make prediction of a new point (especially one extrapolated outside the range of the current points) worse, not better.

Here is an example. The observations for 6 time-points are plotted. What is our prediction for the next time-point? The 4 trend-lines are polynomials fitted to the observations. The higher-order is the polynomial, the better is its the fit to the existing points, but, beyond the quadratic, the worse the prediction of the next point.

In Rasch, we are fitting data to models, so the Rasch equivalent to overfit due to over-parameterization is overfit due to redundancy (over-predictability) in the data.

Based on a comment by Steve Walter, Graduate Institute of Applied Linguistics.

Conceptualizing Overfit or Over-parameterization … S. Walter, Rasch Measurement Transactions, 2008, 22:2 p. 1165

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt222b.htm

Website: www.rasch.org/rmt/contents.htm