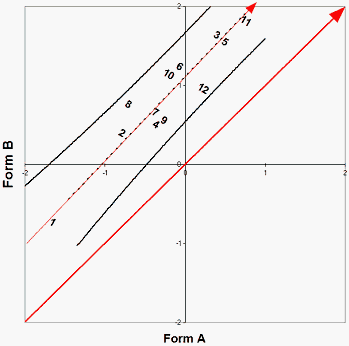
Figure 1. Exact common-item equating
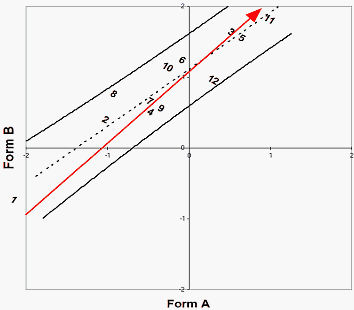
Figure 2. Statistically-equivalent equating

Figure 3. Fahrenheit-to-Celsius Equating
 Figure 1. Exact common-item equating |
 Figure 2. Statistically-equivalent equating |
 Figure 3. Fahrenheit-to-Celsius Equating |
If some items are the same in two different tests, then these may be chosen as "common items". When we perform a Rasch-analysis of the each test separately, we will obtain an estimate of the item difficulty of each common item on each test.
We expect that a scatterplot of the pairs of item estimates for the common items will have a trend line effectively parallel to the identity line. Figure 1 shows this situation in which the 12 common items lie along a trend line (dotted) parallel to the identity line (arrows). 0.0 logits for Form A (x-axis) corresponds to 1.1 logits for Form B (y-axis). To equate Form B with Form A, we subtract 1.1 logits from the Form B item and person measures.
But the trend line may not be parallel to the identity line. What do we do? Figure 2 shows a situation in which the trend line is not a line (arrow) parallel to the identity line. But the arrow falls with in the 95%-confidence error bands (black curves). We cannot reject the hypothesis that the trend line is statistically parallel to the identity line.
Under these circumstances, there are two ways forward.
1. We can choose the Form which we consider to be more definitive. Then obtain its item difficulties and Rasch-Andrich thresholds. Use these values as anchor (fixed) values in an analysis of the other Form. This puts the measures of the second form into the measurement frame-of-reference of the first form.
or 2. We can combine the data from the two Forms into one analysis (concurrent equating) in which all the items and persons are measured in the same frame-of-reference.
Figure 3 shows the situation in which the trend line (dotted line) is obviously and statistically not parallel to the identity line (arrow). Now we have tests of different discrimination, and a "Fahrenheit-to-Celsius" (F-C) equating situation, similar to that encountered with temperature conversions. The "Fahrenheit" measures on Form B needs to be rescale as "Celsius" measures compatible with Form A. An equation for doing this is:
Form B rescaled as Form A = (mean of Form A common items) + (Form B measure - mean of Form B common items) * S.D. of Form A common items / S.D. of Form B common items.
If we have two tests with common items that we know to be functionally different (such as from different test publishers, or in different presentation formats) then we expect to do F-C equating.
If we have two tests with common items that are supposed to be the same (such as alternate test forms, or pre-test and post-test forms), then we are reluctant to do F-C equating. We usually decide which form is the "correct" form (or combine the two forms) and use it as the basis for the equating.
(Suggested by Mg. Andrés Burga León, Ministerio de Educación del Perú)
Common-Item (or Common Person) Equating with Different Test Discriminations … Andrés Burga León, Rasch Measurement Transactions, 2008, 22:3, 1172
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt223d.htm
Website: www.rasch.org/rmt/contents.htm