Advanced DIF Analysis with Winsteps

Winsteps users: do you suffer from RUMM2020 envy? Do you wish you could enjoy the nifty non-uniform DIF detection features that only RUMM2020 users get? Do you wish you could break down the expected responses to polytomous items, and plot them by measure level the way they do it in RUMM2020? RUMM2020 has some very cool features, but Winsteps users do not need to left out in the cold. Thanks to the freely available, open-source data analysis and graphics system, R, Winsteps users can do non-uniform DIF analysis and graphing at least as well as you can with RUMM2020.

R is an open-source implementation of the S language, which was developed at Bell Laboratories. Versions are available for free download for Unix, Windows and MacOS X from www.r-project.org. R comes with a wide range of built-in functions. But since it is a very powerful programming language, extensions can be written to do practically anything. There are at least 1600 contributed packages already available to do almost anything you can think of. At least three packages do Rasch analysis. If you can't find a package already written that will do what you need, you can always write your own. That is what I did in this case.

I have been using the standardized item difficulty difference method of DIF detection for many years. This is fine for dichotomous items, and for uniform DIF in polytomous items, but I began to suspect that groups of survey respondents were responding differently depending on their position on the scale. Since I do not have RUMM, I decided on a DIY approach.

The R program I wrote accomplishes the task like this:

1) Calculates the probability of responding in each of the categories.

2) Calculates the expected response for each person using the category probabilities.

3) Calculates standardized residuals of actual responses from expected responses by group for ranges along the scale.

4) Does 2-way ANOVA on the residuals by group and scale range, with an interaction term.

5) Plots the expected score ogive and the empirical score curves for each group and displays the results of the ANOVA in the graph.

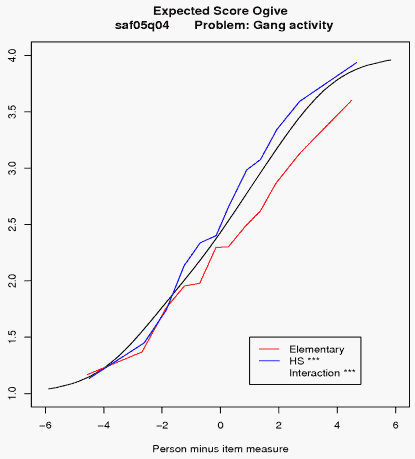
The Figure is an example of such a plot. This item is part of a scale measuring teachers' perceptions of crime and disorder in the school. Teachers are asked to state how much of a problem they perceived gang activity to be.

The black line is the expected score ogive; the blue line is the empirical responses from high school teachers; the red line, the responses from elementary school teachers. At the very low end of the scale, there is very little difference between the responses of high school and elementary teachers. However, at the high end of the scale, high school teachers report that gang activity is more of a problem than elementary school teachers do. The asterisks by "High School" in the legend indicate that the difference between high school and elementary teachers, overall, is very significant. In addition, the asterisks by "Interaction" indicate that the difference across the range of the scale is also significant.

The R program for DIF graphing is available at home.uchicago.edu/~lupp/all-DIF.R

It is heavily commented, but will need modification because the group selection mechanism is unique to each person's situation.

R Statistics - www.r-project.org

RUMM2020 - www.rummlab.com.au

Winsteps - www.winsteps.com

Stuart Luppescu

Consortium on Chicago School Research

University of Chicago

Advanced DIF Analysis with Winsteps … S. Luppescu, Rasch Measurement Transactions, 2008, 22:3, 1173

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt223e.htm

Website: www.rasch.org/rmt/contents.htm