Murphy's law and one-step (concurrent) item banking

As we discuss one-step (concurrent) item banking, let me use an analogy based on the way Michelangelo selected the marble for his masterpieces. He traveled to the quarry and checked blocks until he found one within which he could see the figure. Then, as he worked the marble, he simply chipped away at the parts of the block which did not belong to the figure. You all write with the creative genius that sees the figure in the block, while I work with the chisel and hammer, hoping I don't knock off an ear or nose by mistake.

While Heisenberg's Uncertainty Principle applies in my world, Murphy's law reigns supreme. Everything done in field testing seems to affect my results, usually for the worse. Everyday occurrences like an unplanned fire exercise that shortens a testing period, a substitute teacher who gives wrong instructions, or a teacher who tells students that the test isn't important have changed my data. Therefore, I maintain a healthy skepticism, with a touch of paranoia, until the data prove their consistency and accuracy. Having experienced the myriad of things that can go wrong, I cringe at those AERA sessions where researchers don't cross-validate their analyses or don't bother to use scatter-plots and histograms to screen their data before they apply fragile multivariate analyses.

With the infinity of possible errors in mind, I feel obliged to reject any single step statistical approach, even MSCALE. In my experience, most errors do not follow the benign normal distribution and counter- balance each other. When 20 classes take a test and three do not have time to finish because of a surprise fire drill, the error is purposeful, non-symmetric and darned hard to find. Like Michelangelo, I want to chip away that purposeful error so the true relationship in the data can emerge.

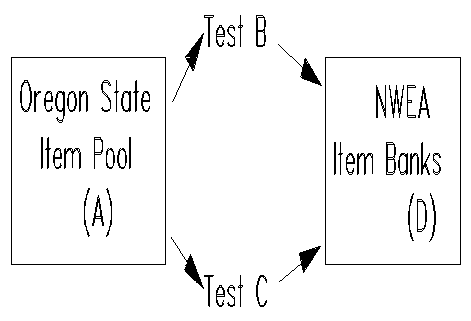
In the course of building the Northwest Association item banks, we ran into many horror stories. For example, we designed a field study to link items from the Oregon State Department to the Rasch reading item bank scales which had been developed in Portland. We used two tests providing a cross-validation of the link between the State item pool and the Portland item bank (see the Figure above). The items passed point biserial and fit criteria, yet the two indirect links, A-B-D and A-C-D, differed by ten RITs (10 RITs = 1 logit), about five times the acceptable amount. Digging deeper, we located the problem. We had designed the tests for fifth graders, but one of the parochial schools "helped us out" by using their eighth grade honors students who averaged 98% across the test. When these students mixed with seven bona fide classes, the statistical analyses appeared just fine. In fact, if we hadn't built in the cross-validation, the error might never have been caught. After dropping the questionable data, the analysis converged with less than an RIT (Rasch unIT = .1 logit) difference in the two links. The point is, the error in this study was non-random, non- symmetric and virtually invisible to the statistical analyses, yet it gummed up the works.

Another reason I prefer a multi-step procedure is the sheer volume of data which we had to analyze to build practical item banks in reading, mathematics and language of several thousand items. We rarely analyzed fewer than 16 tests at a time and often analyzed as many as 100. By working in several steps, we could isolate and eliminate problem data before moving to calibration or linking, which kept those analyses as clean as possible. It may be possible to do all this work in a single procedure, but the enormity of analyzing 100 tests in one step boggles my imagination. Below is a brief description of the steps we followed:

1. We designed the tests so every item appeared on at least three different forms and there were at least three indirect links of the direct link between any two tests. This procedure ensured that at least 30 different classrooms would take each item and that the question would appear in the context of three different tests.

2. We "quick screened" incoming data to produce a choice distribution and point biserial analysis and check that the answer key was correct, that the items had been printed accurately in the test booklets and that the answer sheets had been filled in and scanned properly. We used the results to drop data with these problems from further analysis.

3. We "quick reported" results to teachers within a week of receiving answer sheets. This paid them back for their help and encouraged their voluntary cooperation with future field testing.

4. We "quick classed" the data for each test to produce a "PROX" matrix of item calibrations for each class and searched for items which fluctuated wildly across classes or classes that didn't match the others. This uncovered problems related to the administration of the test such as the fire drill, and substitute teacher syndromes mentioned above. We used the results either to fix the data or to drop those classes which appeared to produce inconsistent results from further analysis.

5. We calibrated the data, plotting actual and theoretical item curves which pinpointed failures of the data to fit the model. We used the results to drop misfitting items from further consideration.

6. We linked the tests through shared items to identify those questions that didn't work the same way on the different forms. We used the results to drop those items from the link and get as accurate a value as possible.

7. We cross-validated every direct link with three or more indirect links (sometimes there were dozens of indirect links). This procedure identified tests and linking values which did not match the scale we were creating, even though the data managed to slip through steps 1 to 6 above. We refined these values until the network was consistent across all the tests that were being analyzed.

8. We linked each test to the permanent Rasch curriculum scale using the calibrations from step 5 and the validated linking values from step 7.

9. We never cheated by short-cutting these steps because we knew that once an error got into the system it would compromise the item bank scales and we might never get rid of it.

These procedures turned up hundreds of errors, most explainable, some mysterious, but all very real. Worst of all, these errors were not random; they acted to depress results and distort both the calibrations and the scales. After experiencing the multitude of things that can go wrong, I believe researchers who link tests without cross-validation or calibrate without screening are too trusting.

My final criticism of one-step (concurrent) procedures is that they foster a belief in magic. Many errors are mundane; items are miskeyed, administrations are botched, data files are truncated during transfer, test codes are incorrectly entered, etc. Specialized tools can detect and remedy these errors quickly, while one step procedures bury them in estimates and error terms. The simplicity of a streamlined one- step approach is appealing, but the final accuracy of the analysis is more important.

I need to except the work of Richard Smith at the American Dental Association from the criticisms above. He analyzes the fit matrix to identify many of the problems I've discussed above, and then reports the information to administrators so it can be used to help dental candidates. Using a multi-step analysis of fit, he really digs into his data. While I could quibble about differences in our style, I believe that anyone using MSCALE will find his ideas of value.

Finally, like Michelangelo, I believe we need to position ourselves between two planes of existence. Theoretically, we must hold fast to the Platonic ideal of true measurement. Then experientially, we must use all of our craft to chip away at the errors that obscure and distort that ideal.

Fred Forster

Murphy's law and one-step (concurrent) item banking. Forster F. … Rasch Measurement Transactions 2:2 p.20-21

Murphy's law and one-step (concurrent) item banking. Forster F. … Rasch Measurement Transactions, 1988, 2:2 p.20-21

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt22d.htm

Website: www.rasch.org/rmt/contents.htm