Bayesian Estimation for the Rasch Model using WinBUGS

In this brief note, we introduce a Bayesian approach to estimating parameters for IRT using a freeware called WinBUGS. We use simple Rasch model below to illustrate such an approach and summarize its benefits at the end, as compared with the use of proprietary software (e.g. WINSTEPS and BILOG).

Simple Dichotomous Rasch Model

A student i will score 1 from answering an item k correctly; 0 otherwise. Let y_ik be the score. Using Simple Rasch Model, we have

y_ik ~ Bernoulli(p_ik)

logit(p_ik) = θ_i - d_k

where θ_i is the ability of student i

d_k is the difficulty of item k.

Formulation of the Rasch Model in WinBUGS

The BUGS (Bayesian inference Using Gibbs Sampling) project is concerned with flexible software for the Bayesian analysis of complex statistical models using Markov chain Monte Carlo (MCMC) methods. WinBUGS is a freeware, which provides graphical interface to access all these modeling utilities.

The first step using WinBUGS is to specify the model concerned and the prior distributions for the unknown parameters. For the simple Rasch model, this is shown in the box below.

The posterior distribution of the unknown parameters can then be obtained by running the model in WinBUGS with the response data.

Bayesian Graphical Modeling of the Rasch Model

In Bayesian graphical modeling, the simple Rasch model is represented in Figure 1.

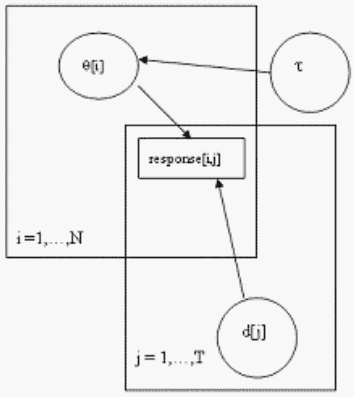
Figure 1. Bayesian Graph of the Rasch Model

The known data response[i,j] is represented in rectangular form. The unknown parameters (θ[i], d[i,j], τ) are represented in circular form. The dependency amongst the data and parameters are shown using directed arrows.

Such a graphical illustration can enhance understanding of the model by others; especially for a more complex model.

WinBUGS specification of the Rasch dichotomous model model { # Simple Rasch Model in WinBUGS for (i in 1 : N) { # Total number of students: N for (k in 1 : T) { # Total number of items: T response[i, k] ~ dbern(p[i, k]) # Response follows a Bernoulli distribution logit(p[i, k]) <- theta[i] - d[k] } # The transformed prob. equals to difference between } # student ability and # item difficulty   # Prior distributions for unknown parameters for (i in 1:N) {theta[i] ~ dnorm(0, tau)} # prior distribution for student abilities for (k in 1:T) {d[k] ~ dnorm(0, 0.001)} # prior distribution for item difficulties tau ~ dgamma(0,001, 0.001) # prior distribution for precision of student abilities sigma<-1/sqrt(tau) # calculate the standard derivation from precision }

Empirical Results and Model Checking

We illustrate our approach using the classical example in educational testing - the Law School Admission Test (LSAT) data, which is available in the R package called ltm (Latent Trait Model). The data contain responses of 1000 individuals to five items which were designed to measure a single latent ability. Here are the results obtained using WinBUGS. "ltm" are the R statistics as estimates for reference.

Estimates of Item difficulty
Item	mean	sd	2.5%	median	97.5%	ltm
1	-2.74	0.13	-3.00	-2.74	-2.49	-2.87
2	-1	0.08	-1.15	-1	-0.84	-1.06
3	-0.24	0.07	-0.38	-0.24	-0.1	-0.26
4	-1.31	0.08	-1.47	-1.31	-1.14	-1.39
5	-2.1	0.11	-2.31	-2.1	-1.9	-2.22

We can see that the estimated values from WinBUGS are close to the ones from ltm which uses a Marginal Maximum Likelihood (MMLE) approach. As the observed data are discrete, one common method of model checking in Bayesian approach is to draw samples from posterior predictive distribution and compare the simulated frequencies of different possible outcomes with the observed ones. Here are the results of model checking.

The model checking statistics are displayed in the graph below. The observed frequencies are shown by a dashed line. The expected frequencies are shown by vertical bars. We can conclude that the observed outcomes are very close to the predicted ones.

	Obs Freq	Expected Frequency
Score		mean	sd	2.5%	median	97.5%
0	3	2.4	1.6	0	2	6
1	21	20.6	5.1	11	20	31
2	87	88.2	9.7	70	88	107
3	240	228.1	14.5	200	228	256
4	361	366.0	17.1	333	366	399
5	303	294.8	17.6	261	295	330

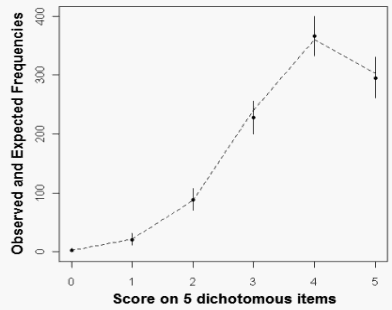
Figure 2. Observed and Expected Frequencies

Flexibility in Enhancing the Model

WinBUGS allows a great flexibility in modeling. For example, we could easily enhance the modeling of student abilities θ_i with other covariates X_ti, if such information is available. One of the possible formulations could be:

θ_i ~ N(μ_i, σ_θ²)

where μ_i = β₀ + Σ_tβ_tX_ti and σ_θ²~IG(0.001,0.001).

The WinBUGS code above could be modified easily to incorporate such an enhancement. Parameter estimation in the enhanced model could be automatically taken care by WinBUGS.

Summary

As compared with the proprietary software, the advantages of using the WinBUGS include the following:

(1) the Rasch model can be displayed in a graphical display to facilitate communication and understanding;

(2) testing statistics for model checking could be tailored for the problem at hand; and

(3) a great flexibility in modeling is provided.

Dr. Fung Tze-ho
Manager-Assessment Technology & Research,
Hong Kong Examinations and Assessment Authority
www.hkeaa.edu.hk/en

---

Tze-ho F. (2009) Bayesian Estimation for the Rasch Model using WinBUGS, Rasch Measurement Transactions, 2009, 23:1, 1190-1

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt231e.htm

Website: www.rasch.org/rmt/contents.htm