RMT 23:1 Notes and Quotes

Georg Rasch, Factor Analysis and Scales

[Georg] Rasch was strongly against exploratory factor analysis, for two reasons. Not only because it was based on unrealistic assumptions like linearity and normality, but also because it was exploratory. He therefore always stressed that Rasch analysis is confirmatory. That it does require a theory of the construct and that the purpose of the analysis was both to check the theory and to check the items.

And Rasch never talked about interval scales. To Rasch, the constructs that we measure by Rasch models are constructs on ratio scales with absolute zeros and arbitrary units. Taking the logarithm of a ratio scale measure ["for practical purposes", Rasch, 1980, p.80] creates something similar to an interval scale since the arbitrary unit of the ratio scale is transformed into an arbitrary origin of the logit scale. An arbitrary unit on the logit scale corresponds to an arbitrary power transformation on the ratio scale, which is rarely taken to be part of the definition of ratio scales.

Svend Kreiner

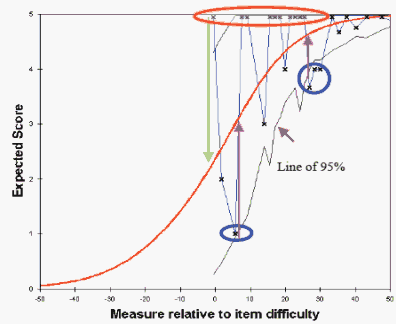
Item Characteristic Curves: Model and Empirical. Figure 3 in Rashid et. al (2008) WSEAS Transactions on Advance in Engineering Education, 8, 5, 591-602

---

Infit Mean-squares: Mean ± 2 S.D.

"There are no hard-and-fast rules for setting upper- and lower-control limits for the infit statistics (i.e., infit mean-square index). In general, as Pollitt and Hutchinson (1987) suggest, any individual infit mean-square value needs to be interpreted against the mean and standard deviation of the set of infit-mean square values for the facet concerned. Using these criteria, a value lower than the mean minus twice the standard deviation would indicate too little variation, lack of independence, or overfit. A value greater than the mean plus twice the standard deviation would indicate too much unpredictability, or misfit." (Park, 2004)

Comment: This advice accords with an investigation into "Do the data fit the model usefully". The mean-squares are geometric with a range of 0-1-∞, which suggests that the computation of mean and standard deviation should be done using log_e(mean-squares). In general, overfit (low mean-square) is generally a much smaller threat to the validity of the measures than excessive unpredictability (high mean-square).

Park, T. (2004) An investigation of an ESL placement test using Many-Facet Rasch Measurement. Teachers College, Columbia University Working Papers in TESOL and Applied Linguistics, 4, 1

journals.tc-library.org/index.php/tesol/article/view/41/48

Pollitt, A., & Hutchinson, C. (1987). Calibrated graded assessment: Rasch partial credit analysis of performance in writing. Language Testing, 4, 72-92.

---

Various (2009) Notes and Quotes, Rasch Measurement Transactions, 2009, 23:1, 1197

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt231l.htm

Website: www.rasch.org/rmt/contents.htm