The Concept of a Measurement Mechanism

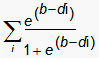
"And in technology, as well as in basic science, to explain a fact is to exhibit the mechanism(s) that makes the system in question tick" (Bunge, 2004, p. 182).

In 1557, the Welshman Robert Recorde remarked that no two things could be more alike (i.e., more equivalent), than parallel lines and thus was born the equal sign, as in 3 + 4 = 7. Equation (1) is the familiar Rasch model for dichotomous data, which sets a measurement outcome (raw score) equal to a sum of modeled probabilities. The measurement outcome is the dependent variable and the measure (e.g., person parameter, b) and instrument (e.g., item parameters di's) are independent variables. The measurement outcome (e.g., count correct on a reading test) is observed, whereas the measure and instrument parameters are not observed but can be estimated from the response data. When a mechanismic interpretation¹ is imposed on the equation, the right-hand side (r.h.s.) variables are presumed to characterize the process that generates the measurement outcome on the left-hand side (l.h.s.). An illustration of how such a mechanism can be exploited is given in Stone (2002). The item map for the Knox cube test analysis had a 1 logit gap. The specification equation was used to build an item that theory asserted would fill in the gap. Subsequent data analysis confirmed the theoretical prediction of the Rasch relationship:

Raw score =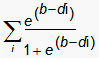

(1)

Typically, the item calibrations (di's) are assumed to be known, and the measure parameter is iterated until the equality is realized (i.e., the sum of the modeled probabilities equals the measurement outcome). How is this equality to be interpreted? Are we only interested in the algebra or is something more happening?

Freedman (1997) proposed three uses for a regression equation like the one above:

1.1) To describe or summarize a body of data,

2.2) To predict the l.h.s. from the r.h.s,

1.3) To predict the l.h.s. after manipulation or intervention on one or more r.h.s. variables (measure parameter and/or instrument parameters).

Description and summarization possess a reducing property in that they abstract away incidentals to focus on what matters in a given context. In a rectangular persons-by-items data matrix (with no missing data), there are np x ni observations. Equations like those above summarize the data using only np + ni - 1 independent parameters. Description and summarization are local in focus. The relevant concept is the extant data matrix with no attempt to answer questions that might arise in the application realm² about "what if things were different." Note that if interest centers only on the description and summary of a specific data set, additional parameters can be added, as necessary, to account for the data.

Prediction typically implies the use of the extant data to project into an as yet unobserved context/future in the application realm. For example, items from the extant data are used to compute a measure for a new person, or person parameters are used to predict how these persons will perform on a new set of items. Predictions like these rest on a set of claims of invariance. New items and new persons are assumed to behave as persons and items behaved in the extant data set. Rasch fit statistics (for persons and items) are available to test for certain violations of these assumptions of invariance (Smith, 2000).

Rasch models are probabilistic models that are fundamentally associational and thus cannot and do not, alone, support a causal interpretation of equation (1) (Woodward, 2003). Note that equation (1) can support a predictive interpretation if the equality is taken to satisfy a simple if-then condition. A causal interpretation of equation (1) requires successful predictions under manipulation of the measure parameter, the instrument parameters, or ideally, under conjoint manipulation of the two parameters. Conjoint manipulation up and down the scale directly tests for the trade-off property that holds only when the axioms of additive conjoint measurement are satisfied (Kyngdon, 2008).

To explain how an instrument works is to detail how it generates the count it produces (measurement outcome) and what characteristics of the measurement procedure affect that count. This kind of explanation is neither just statistical nor synonymous with prediction. Instead, the explanation entails prediction under intervention: if I wiggle this part of the mechanism, the measurement outcome will be different by this amount. As noted by Hedström (2005), "Theories based on fictitious assumptions, even if they predict well, give incorrect answers to the question of why we observe what we observe" (p. 108). Rasch models, absent a substantive theory capable of producing theory-based instrument calibrations, may predict how an instrument will perform with another subject sample (invariance) but can offer only speculation in answer to the question, "How does this instrument work?" Rasch models without theory are not predictive under intervention and, thus, are not causal models.

Measurement mechanism is the name given to just those manipulable features of the instrument that cause invariant measurement outcomes for objects of measurement that possess identical measures. A measurement mechanism explains by opening the black box and showing the cogs and wheels of the instrument's internal machinery. A measurement mechanism provides a continuous and contiguous chain of causal links between the encounter of the object of measurement and instrument and the resulting measurement outcome (Elster, 1989). We say that the measurement outcome (e.g., raw score) is explained by explicating the mechanism by which the measurement outcome is brought about. In this view, to respond with a recitation of the Rasch equation for converting counts into measures, to reference a person by item map, to describe the directions given to the test-taker, to describe an item-writing protocol, or simply to repeat the construct label more slowly and loudly (e.g., extroversion), provides a nonanswer to the question, "How does this instrument work?"

Although the sociologist Peter Hedström (2005) was concerned with the improvement of macro theory, several of his reasons for favoring mechanistic explanations apply to measurement science in general:

2.1) Detailed specifications of mechanisms result in more intelligible explanations.

2.2) A focus on mechanisms rather than, for example, item types, reduces theoretical fragmentation by encouraging consideration of the possibility that many seemingly distinct instruments (e.g., reading tests) with different item types and construct labels may in fact share a common measurement mechanism.

2.3) The requirement for mechanistic explanations helps to eliminate spurious causal accounts of how instruments work.

Measurement mechanisms as theoretical claims make point predictions under intervention: when we change (via manipulation or intervention) either the object measure (e.g., reader experiences growth over a year) or measurement mechanism (e.g., increase text measure by 200L). The mechanismic1 narrative and associated equations enable a point prediction on the consequent change in the measurement outcome (i.e., count correct). Notice how this process is crucially different from the prediction of the change in the measurement outcome based on the selection of another, previously calibrated instrument with known instrument calibrations. Selection is not intervention in the sense used here. Our sampling from banks of previously calibrated items is likely to be completely atheoretical, relying, as it does, on empirically calibrated items/instruments. In contrast, if we modify the measurement mechanism rather than select previously calibrated measurement mechanisms, we must have intimate knowledge of how the instrument works. Atheoretical psychometrics is characterized by the aphorism "test the predictions, never the postulates" (Jasso, 1988, p. 4), whereas theory-referenced measurement, with its emphasis on measurement mechanisms, says test the postulates, never the predictions. Those who fail to appreciate this distinction will confuse invariant predictors with genuine causes of measurement outcomes.

A Rasch model combined with a substantive theory embodied in a specification equation provides a more or less complete explanation of how a measurement instrument works (Stenner, Smith, & Burdick, 1983). A Rasch model in the absence of a specified measurement mechanism is merely a probability model; a probability model absent a theory may be useful for (1.1) and (1.2), whereas a Rasch model in which instrument calibrations come from a substantive theory that specifies how the instrument works is a causal model; that is, it enables prediction after intervention (1.3):

"Causal models (assuming they are valid) are much more informative than probability models: A joint distribution tells us how probable events are and how probabilities would change with subsequent observations, but a causal model also tells us how these probabilities would change as a result of external interventions. . . . Such changes cannot be deduced from a joint distribution, even if fully specified." (Pearl, 2000, p. 22)

A mechanismic narrative provides a satisfying answer to the question of how an instrument works. Below are two such narratives for a thermometer designed to take human temperature (3.1) and a reading test (3.2).

3.1) "The Nextemp thermometer is a thin, flexible, paddle-shaped plastic strip containing multiple cavities. In the Fahrenheit version, the 45 cavities are arranged in a double matrix at the functioning end of the unit. The columns are spaced 0.2°F intervals covering the range of 96.0°F to 104.8°F. . . . Each cavity contains a chemical composition comprised of three cholesteric liquid crystal compounds and a varying concentration of a soluble additive. These chemical compositions have discrete and repeatable change-of-state temperatures consistent with an empirically established formula to produce a series of change-of-state temperatures consistent with the indicated temperature points on the device. The chemicals are fully encapsulated by a clear polymeric film, which allows observation of the physical change but prevents any user contact with the chemicals. When the thermometer is placed in an environment within its measure range, such as 98.6°F (37.0°C), the chemicals in all of the cavities up to and including 98.6°F (37.0°C) change from a liquid crystal to an isotropic clear liquid state. This change of state is accompanied by an optical change that is easily viewed by a user. The green component of white light is reflected from the liquid crystal state but is transmitted through the isotropic liquid state and absorbed by the black background. As a result, those cavities containing compositions with threshold temperatures up to and including 98.6°F (37.0°C) appear black, whereas those with transition temperatures of 98.6°F (37.0°C) and higher continue to appear green" (Medical Indicators, 2006, pp. 1-2).

3.2) "The MRW technology for measuring reading ability employs computer generated four-option multiple choice cloze items "built on-the-fly" for any continuous prose text. Counts correct on these items are converted into Lexile measures via an applicable Rasch model. Individual cloze items are one-off and disposable. An item is used only once. The cloze and foil selection protocol ensures that the correct answer (cloze) and incorrect answers (foils) match the vocabulary demands of the target text. The Lexile measure of the target text and the expected spread of the cloze items are given by a proprietary text theory and associated equations. A difference between two reader measures can be traded off for a difference in Lexile text measures to hold count correct (measurement outcome) constant. Assuming a uniform application of the item generation protocol the only active ingredient in the measurement mechanism is the choice of text with the requisite semantic (vocabulary) and syntactic demands."

In the first example, if we uniformly increase or decrease the amount of additive in each cavity, we change the correspondence table that links the number of cavities that turn black to a degree Fahrenheit. Similarly, if we increase or decrease the text demand (Lexile) of the passages used to build reading tests, we predictably alter the correspondence table that links count correct to Lexile reader measure. In the former case, a temperature theory that works in cooperation with a Guttman model produces temperature measures. In the latter case, a reading theory that works in cooperation with a Rasch model produces reader measures. In both cases, the measurement mechanism is well understood, and we exploit this understanding to answer a vast array of "W" questions (see Woodward, 2003): If things had been different (with the instrument or object of measurement), what then would have happened to what we observe (i.e., the measurement outcome)?

To explain a measurement outcome, "One must provide information about the conditions under which [the measurement outcome] would change or be different. It follows that the generalizations that figure in explanations [of measurement outcomes] must be change-relating. . . . Both explainers [e.g., person parameters and item parameters] and what is explained [measurement outcomes] must be capable of change, and such changes must be connected in the right way." (Woodward, 2003, p. 234)

The Rasch model tells us the right way that object measures, instrument calibrations, and measurement outcomes are to be connected. Substantive theory tells us what interventions/changes can be made to the instrument to offset a change to the measure for an object of measurement to hold constant the measurement outcome. Thus, a Rasch model in cooperation with a substantive theory dictates the form and substance of permissible conjoint interventions. A Rasch analysis, absent a construct theory and associated specification equation, is a black box and "as with any black-box computational procedures, the illusion of understanding is all too easy to generate". (Humphreys, 2004, p. 132).

A. Jackson Stenner, Mark H. Stone, Donald S. Burdick

Footnotes

1. The term mechanismic was coined by Bunge (2004) to emphasize the nonmechanical features of some mechanisms.

2. In applied mathematics, we typically distinguish between the mathematical realm and the application realm.

References

Bunge, M. (2004). How does it work? The search for explaining mechanisms. Philosophy of Social Science 34, 182-210.

Elster, J. (1989). Nuts and bolts for the social sciences. Cambridge, MA: Cambridge University Press.

Freedman, D. (1997). From association to causation via regression. In V. McKim & S. Turner (Eds.), Causality in crisis? Statistical methods and the search for causal knowledge in the social sciences (pp. 113-161). Notre Dame, IN: University of Notre Dame Press.

Hedström, P. (2005). Dissecting the social: On the principles of analytical sociology. Cambridge, UK: Cambridge University Press.

Humphreys, P. (2004). Extending ourselves: Computation science, empiricism, and scientific method. New York: Oxford University Press.

Jasso, G. (1988). Principles of theoretical analysis. Sociological Theory, 6, 1-20.

Kyngdon, A. (2008). Conjoint measurement, error and the Rasch model: A Reply to Michell, and Borsboom and Zand Scholten. Theory and Psychology, 18(1),125-131

Kyngdon, A. (2008). The Rasch model from the perspective of the representational theory of measurement. Theory and Psychology, 18(1), 89-109.

Medical Indicators. (2006). [Technical paper]. www.medicalindicators.com

Pearl, J. (2000). Causality: Models, reasoning, and inference. Cambridge, MA: Cambridge University Press.

Smith, R. M. (2000). Fit analysis in latent trait measurement models. Journal of Applied Measurement, 1(2), 199-218.

Stenner, A. J., Smith, M., & Burdick, D. (1983). Toward a theory of construct definition. Journal of Educational Measurement, 20 (4), 305-316.

Stone, M. H. (2002). Knox's cube test: Revised. Wood Dale, IL: Stoelting.

Woodward, J. (2003). Making things happen. New York: Oxford University Press.

Stenner A.J., Stone M.H., Burdick D.S. (2009) The Concept of a Measurement Mechanism, Rasch Measurement Transactions, 2009, 23:2, 1204-6

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt232b.htm

Website: www.rasch.org/rmt/contents.htm