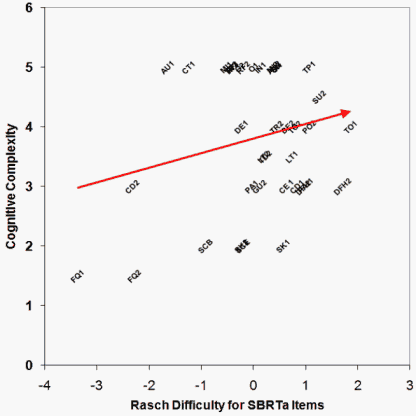
Theoretical Complexity vs. Rasch Item Difficulty in Reading Tests

The concept of unidimensionality of reading comprehension (Weir & Porter, 1994) has led scholars to believe that there might be a one-to-one correspondence between item difficulty and the level of cognition the item measures (Alderson, 1990). It is commonplace among reading specialists to divide reading ability into different layers of cognition such that hypothetically labeled lower layers are assumed to be followed by higher ones (Alderson, 1990). The hierarchy assumption is so appealing that tests developers usually calibrate items solely in terms of item difficulty, while ignoring issues related to their level of cognition. Yet, it is often the case that more difficult items represent lower order abilities (at least as predicted by theory) than do easier ones (Weir and Porter, 1994). Paradoxically, harder items seem to contribute less to reading ability than do easier ones (Meyer, 1975, cited in McNamara, 1996).

Weir and Porter (1994) suggest that the main reason for limiting the reproducibility assumption to item difficulty in test constructions is 'practical expediency rather than ... a principled view of unidimensionality' (p. 9). Because empirical item hierarchies sometimes contradict theoretical notions of reading comprehension (McNamara, 1996; Weir & Porter, 1994; Alderson, 1990), we approach the issue from a qualitative as well as a quantitative perspective:

1. Does there exist a one-to-one correspondence between item difficulty and the nature of the latent ability the item measures?

2. To what extent do variations in item difficulty reflect qualitative rather than quantitative item differences?

Figure 1. Theoretical Complexity vs. Rasch Difficulty.

To address these questions we used the SBRT - Forms a and b - which are (mostly) multiple-choice item language tests. The SBRT was developed at the Iran University of Science and Technology (IUST) (Daftarifard, 2000) using over 200 intermediate students for each form. As is shown in Table 1, the SBRTa contains 39 questions that address twenty-four abilities that are frequently referred to in the literature. Items' hypothetical cognitive complexity is indicated by the ordinal number in the last column of this table. The classification of some items is uncertain (e.g., answering factual questions might either be classified as perception or speed reading).

Reading ability as a hierarchy

The results in Table 1 and Figure 1 reveal a clear lack of correspondence between item complexity and the hypothetical level of cognition. Some supposedly cognitively demanding abilities turned out to be less difficult than less cognitively demanding abilities, and some item types are out of order. This is summarized by the finding that the Spearman rank correlation between items' Rasch locations and their hypothetical complexity is just 0.22. Moreover, the average locations for items in complexity groups 1 or 2, 2, 3, 3 or 4, 4, 4 or 5, and 5, are -2.8, -0.2, 0.4, 0.4, 0.8, 1.2, and -0.1 logits, respectively.

The existence of one-to-one relation between empirical (i.e., Rasch) and hypothetical complexity follow is contradicted in many ways. For instance, DFH2 (distinguishing between fact and hypothesis) is harder than IN2 (inferencing), while RF2 (understanding the rhetorical function of the text) is easier than LT1 (understanding the literal meaning). Similarly, the presumably more complex skill of understanding the factual question (here FQ1) is much easier than mere text scanning (both SCB and SCE). Also, skimming (SK1) turns out to be more difficult than SK2 (Rasch measure -0.23) although both belong to speed reading category. Certain items which hypothetically measure higher ability like interpretation ability turn out to be much easier than lower level items like speed reading (here SK1 with the Rasch measure of 0.57). These include items AU1 with Rasch measure of -1.65, CT1 with the Rasch measure of -1.24, MI1 with the Rasch measure of -0.52, TP2 with the Rasch measure of -0.42, RF1 with the Rasch measure of -0.40, and IN2 with the Rasch measure of -0.40.

Another problem found in the data pattern concerns items with the same operational definition but with quite different item difficulties. These items include understanding the audience of the text, i.e., AU1 and AU2 with two different consecutive Rasch measures -1.65 and 0.39, CD1 and CD2 with two consecutive Rasch measures of 0.84 and -2.32, ED1 and DE2 with two different Rasch measures of -0.23 and 0.60 respectively, PA1 and PA2 with two consecutive different Rasch measures of -0.03 and 0.98, and TP1 and TP2 with the Rasch measures of 1.07 and -0.42 respectively. Among these, however, there are only a few items that operationally belong to one category and turn up with almost similar measure like SI1 and SI2 with Rasch measure of 0.45 and 0.43.

We point out that the findings summarized above cannot be attributed to the particular set of items being used. Firstly, the SBRTa items fit the Rasch model adequately (only one item's outfit exceeds 1.3), thus establishing this test-form's measurement validity. Second, in support of unidimensionality, factor analysis of items' Rasch residuals indicates that just three items (SI1, AU2 and SK2) loaded higher than 0.5 on the most prominent residual factor. Third, the SBRTa shows acceptable classical reliability (coefficient alpha = 0.82). Fourth, students' SBRTa measures are highly correlated with their measures on the widely used IELTS (exemplar, 1994, the academic version of module C , r = 0.71, p < .001). Finally, the lack of correlation between items' hypothetical and empirical difficulties is replicated for the second test form, the SBRTb. Similar to the value observed for the SBRTa, the rank correlation for the SBRTb is just 0.23.

The present findings thus indicate that while reading is unidimensional and hierarchical, this hierarchy disagrees with theoretical predictions in the literature (for an overview, see e.g., Alderson, 1990). Given this lack of correspondence, we propose that notions of items complexity require careful distinctions between the qualitative and quantitative aspects of reading theory. For instance, it may be necessary to distinguish between the complexity of a concept and the complexity of the question designed to assess this concept. Rasch scaling is likely to remain the tool of choice in this research, but it seems likely that multi-facetted approaches will be needed to accommodate both types of complexity simultaneously.

Parisa Daftarifard

Rense Lange, Integrated Knowledge Systems

References

Alderson, J. C. (1990). Testing reading comprehension skills (part one). Reading in a Foreign Language, 6(2), 425-438.

Daftarifard, P. (2002). Scalability and divisibility of the reading comprehension ability. Unpublished master's thesis. Tehran, Iran: IUST.

McNamara, T. (1996). Measuring Second Language Performance. New York: Addison Wesley Longman.

Weir C. J., & Porter D. (1994). The Multi-Divisible or Unitary Nature of Reading: The language tester between Scylla and Charybdis. Reading in a Foreign Language, 10(2), 1-19.

Editor's Note: These findings contrast with the remarkable success of the Lexile system at predicting the Rasch item difficulty of reading-comprehension items. See Burdick B., Stenner A.J. (1996) Theoretical prediction of test items. Rasch Measurement Transactions, 1996, 10:1, p. 475. www.rasch.org/rmt/rmt101b.htm

Daftaripard P., Lange R. (2009) Theoretical Complexity vs. Rasch Item Difficulty in Reading Tests, Rasch Measurement Transactions, 2009, 23:2, 1212-3

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt232e.htm

Website: www.rasch.org/rmt/contents.htm