RMT 23:2 Notes and Quotes

How Many Rating-Scale Categories?

"First, scales with two or three response alternatives are generally inadequate in that they are incapable of transmitting very much information and they tend to frustrate and stifle respondents.

"Second, the marginal returns from using more than nine response alternatives are minimal and efforts for improving the measurement instrument should be directed toward more productive areas.

"Third, an odd rather than an even number of response alternatives is preferable under circumstances in which the respondent can legitimately adopt a neutral position. Overuse of the neutral category by respondents can generally be avoided by providing them with an adequate number of reasonable response alternatives. [Ben Wright argued that a neutral category allowed respondents to escape from making difficult or uncomfortable decisions.]

"Fourth, even a few response alternatives may be too many for the respondent if comprehensible instructions and labeling of response alternatives are not included to enable the respondent to conceptualize and respond in spatial terms."

Cox E.P. III (1980) The Optimal Number of Response Alternatives for a Scale: A Review. Journal of Marketing Research, 17, 4, 407-422

DIF Sample Size for Polytomous Items

Scott, Fayers, Aaronson, et al. (2009) A simulation study provided sample size guidance for differential item functioning (DIF) studies using short scales. Journal of Clinical Epidemiology 62, 288-295, make the following recommendations (with many provisos):

Uniform DIF in polytomous items:

"Based on our results, as a general rule of thumb, we would suggest imposing a minimum of 200 respondents per group to ensure adequate performance. If the scale contains just two items, we would suggest a minimum of 300 respondents."

Non-uniform DIF in polytomous items:

500 respondents per group were not enough to detect non-uniform DIF reliably. Further, "it is difficult to know what amount of non-uniform DIF ... represents practically important non-uniform DIF as no published guidelines on this topic were identified."

Foundations of Measurement

suppes-corpus.stanford.edu/measurement.html links to 18 downloadable video lectures on Measurement Theory. They were given in 1981 by Patrick Suppes, R. Duncan Luce, and Amos Tversky. Two of Duncan Luce's lectures are titled "Conjoint Measurement", reminding us of Luce, R. D. and J. W. Tukey. (1964). "Simultaneous Conjoint Measurement: A New Type of Fundamental Measurement," Journal of Mathematical Psychology, 1, 1-27.

Michael Lamport Commons

What is "Scaling" ?

"Scaling" is an ambiguous word in English, even in its psychometric usage.

"Scale" from "scala" (a ladder) is a means of "positioning objects in an ascending sequence (up a ladder)" - so it signifies "ordering".

"Scale" from "skal" (a bowl) is part of the pan-balance, "weight scales", "scales of justice" - so it signifies "quantification".

A "Guttman Scalogram" is a Guttman ordering, not a Guttman quantification. But "Rasch scaling" is a Rasch quantification, which includes a Rasch ordering, but only secondarily.

Measurability does not demonstrate existence

"Valid measures are often taken, albeit implicitly, as proof that the assumed variable really does exist. Suppose one could attain evidence of the unidimensionality and linearity of the QoL scores from a questionnaire: again, this would still not be evidence that the measurable variable named QoL is QoL. Naming a variable is a matter of perspective: it relates to the meaning the variable is assigned, rather than to its intrinsic properties."

Tesio, L. (2009) Quality of life measurement: one size fits all. Journal of Medicine and the Person (2009) 7:5-9

Rasch Measurement And Sociological Theory

"Have you ever pondered the ambiguity of "and" in titles? Here I mean, "Rasch Measurement, a Challenge to Sociological Theory." The challenge is to take seriously a measurement model that is attractive in the light of commonly observed patterns in data and also for its fundamental logical and statistical properties. Taking it seriously will mean exploring carefully the conceptual consequences of the assumptions that all responses are probabilistic and that it is possible to separate the measurement of personal traits (such as attitudes) and the measurement of social objects (such as questionnaire items or social. entities or social values)."

Otis Dudley Duncan (1982) Rasch Measurement And Sociological Theory. Lecture at Yale University.

Web KIDMAP

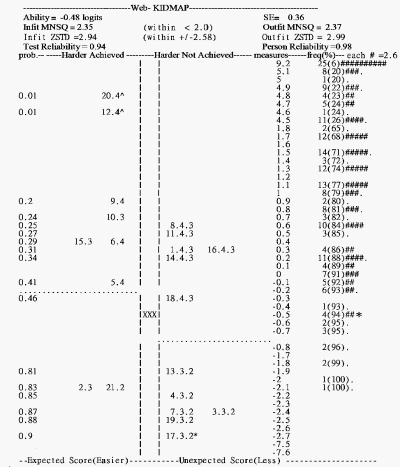
Figure 1 in Tsair-Wei Chien, Weng-Chung Wang, Sho-Be Lin, Ching-Yih Lin, How-Ran Guo and Shih-Bin Su (2009) KIDMAP, a web based system for gathering patients' feedback on their doctors. BMC Medical Research Methodology 2009, 9:38

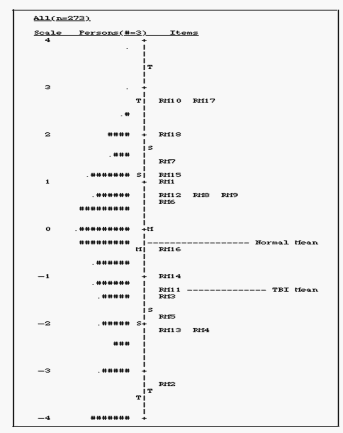
Wright map from Prieto, Gerardo, Delgado, Ana R., Perea, Maria V. and Ladera, Valentina (2009) Scoring Neuropsychological Tests: Using the Rasch Model: An Illustrative Example With the Rey-Osterrieth Complex Figure, The Clinical Neuropsychologist.

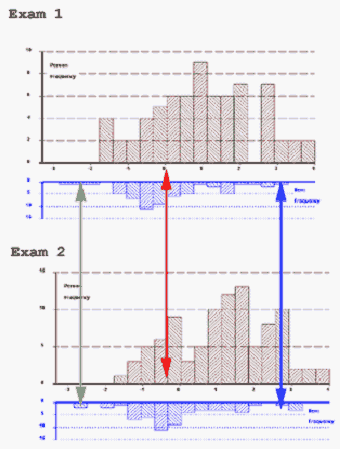
Two tests equated by common person/item linking. Figure in Yu, Chong Ho & Sharon E. Osborn Popp (2005). Test Equating by Common Items and Common Subjects: Concepts and Applications. Practical Assessment Research & Evaluation, 10(4). Available online: pareonline.net/getvn.asp?v=10&n=4

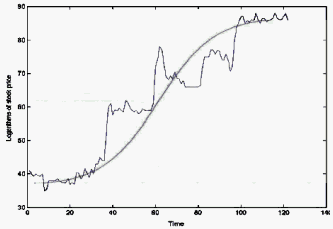
Model and empirical logistic ogives for stock prices. Figures 7 and 17, "Price trajectory for Charter Plc from 22nd April 2003 to 17th October 2003", in Silas N. Onyango (2007) On the pattern recognition of Verhulst-logistic Itô Processes in Market Price Data. Artificial Intelligence and Pattern Recognition ISRST (2007), p. 294-301.

Test Theory Reference Materials Online

"The Reference Supplement to the Manual for relating Language Examinations to the Common European Framework of Reference for Languages (CEFR)" is an online resource on test theory and standard setting, published by the Council of Europe at www.coe.int/t/dg4/linguistic/Manuel1_EN.asp

which includes these sections:

B: Standard Setting by Felianka Kaftandjieva

C: Classical Test Theory by Norman Verhelst

D: Qualitative Analysis Methods by Jayanti Banerjee

E: Generalizability Theory by Norman Verhelst

F: Factor Analysis by Norman Verhelst

G: Item Response Theory (mostly Rasch) by Norman Verhelst

H: Many-Facet Rasch Measurement by Thomas Eckes

I: Cito variation on the bookmark method by Frank van der Schoot

Thomas Eckes

Various (2009) Notes and Quotes, Rasch Measurement Transactions, 2009, 23:2, passim

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt232g.htm

Website: www.rasch.org/rmt/contents.htm