Dichotomizing Rating Scales and Rasch-Thurstone Thresholds

Findings based on rating scales can be difficult to explain to a non-technical audience. If the rating-scale categories can be bisected by a pass-fail cut-point, such as "agree or not", "competent or not", "impaired or not", "success or failure", then it can simplify communication if the rating scale is dichotomized around the cut-point. Categories above the cut-point are scored "1", and categories below the cut-point are scored "0".

How do measures based on the dichotomized data relate to the measures based on the original ratings? The Figure illustrates the relationship.

The Figure shows a 3-category item, rated 0-1-2. The two cumulative probability ogives (based on the Rasch Partial-Credit Model, PCM) for that rating scale are shown. The intersections of the ogives with 0.5 probability are the Rasch-Thurstone thresholds.

The rating scale can be dichotomized in two ways: 0-1-2 becomes 0-0-1 or 0-1-2 becomes 0-1-1. These two dichotomizations can be analyzed with the dichotomous Rasch model. To make comparison simpler, the person measures are anchored at their rating-scale estimates. The result of the dichotomous analysis is two dichotomous ogives, one for each of the two dichotomizations. The Figures indicates that the two dichotomous ogives approximate the cumulative probability ogives of the rating-scale analysis. Thus the difficulties of the dichotomized items approximate the Rasch-Thurstone cumulative-probability thresholds, not the Rasch-Andrich equal-adjacent-category-probability thresholds (which are generally more central).

This result is reassuring because it indicates that inferences based on the simpler dichotomized data approximate inferences based on the more complex rating-scale data.

This also suggest that, when only the top category of a partial-credit scale is "correct", the Rasch-Thurstone threshold of the top category of the partial-credit (rating-scale) item corresponds to the dichotomous difficulty of the equivalent right-wrong item.

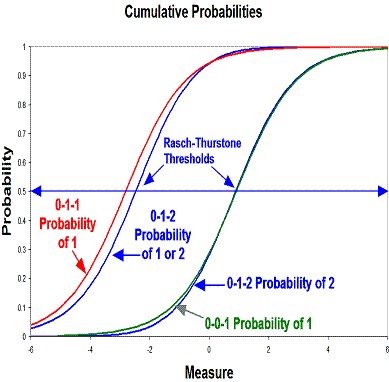
Note: the actual ranges of the categories on the latent variable are given by the 50% Cumulative Probabilities = the Rasch-Thurstone thresholds (not the Rasch-Andrich thresholds). When the interval between two Rasch-Thurstone thresholds is less than about 1.0 logits, the category is no longer modal - the peak probability is lower than the probability of adjacent categories. Todiscover what are the category boundaries on the latent variable, imagine 1000 persons on the latent variable at a category boundary. When they respond, 50% will choose categories below the boundary and 50% above. This happens at the Rasch-Thurstone threshold. It does not happen at the Rasch-Andrich threshold. This is further confirmed by dichotomizing the rating-scale responses - see above. The dichotomized item difficulties are close to the Rasch-Thurstone thresholds, not the usually more central Rasch-Andrich thresholds.

Linacre J.M. (2009) Dichotomizing Rating Scales and Rasch-Thurstone Thresholds, Rasch Measurement Transactions, 2009, 23:3, 1228

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt233e.htm

Website: www.rasch.org/rmt/contents.htm