Re-Parameterization of the Partial Credit Model
for Estimating Items with Large Values of Maximum Marks

The conventional formulation of Partial Credit Model (PCM) is as follows:

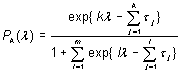
where P_k(λ) is the probability of a student with ability λ obtaining the score k on an item with minimum mark equal to 0 and maximum mark equal to m, and {tj} are the non-centralized thresholds (= centralized threshold + item difficulty).

It can be observed that when the maximum mark of an item equals to m, the number of parameters that need to be estimated is also exactly equal to m. When m is very large (e.g., 20 or 30) which may not be uncommon for a non-multiple-choice item, the number of parameters subject to estimation may cause great problems or even a breakdown of commonly available software. In this brief note, a re-parameterization of PCM is proposed in order to cater for items with large values of maximum marks.

Re-parameterization of PCM

We re-formulate PCM using 4 parameters (S,q, d, c), at most, for items with any values of maximum marks. The idea of the re-formulation is shown in the following diagram:

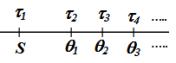
S: The start point

θ: The first interval (i.e., θ1=θ and θi+1=θi+di where i ≥ 1)

d: The change applied to the first interval to obtain the second one (i.e., d1=d)

c: The variation of the change as compared with only the previous change (i.e. di+1=di+c where i ≥ 1)

Note that an approximation (i.e., assuming that the same c is applied for different di) is adopted here. By using the approximation, 4 parameters are enough to generate all the thresholds. The derivations of some thresholds are shown below:

t1 = S

t2 = S + θ1 = S + θ

t3 = S + θ1 + θ2 = (S + θ) + (θ 1+ d1) = S + 2θ + d

t4 = S + θ1 + θ2 + θ3 = (S + 2θ + d) + (θ2+d2) = (S + 2θ + d) + (θ 1+ d1+d1+c) =(S + 2θ + d) + (θ + 2d + c) = S + 3θ + 3d + c

It can be shown (by the use of mathematical induction) that the general form is:

tj = S + (j-1)θ + (j-1)(j-2) d /2 + (j-1)(j-2)(j-3)c /6

Based on the general form, we can immediately derive the following:

= kS + k(k-1)θ /2 + k(k-1)(k-2)d/6 + k(k-1)(k-2)(k-3)c/24

Therefore PCM can now be re-formulated using only the 4 parameters: S,θ, d, c.

Parameter Estimation using WinBugs

The estimation of the re-formulated parameters can be achieved directly using the freeware WinBugs. As an illustration, the relevant code to set up the probability model for an item with maximum mark equal to 18 in WinBugs is shown in Figure 2.

In addition, non-informative prior distributions are set up for the parameters concerned. The corresponding WinBugs code is shown in Figure 3.

Then the parameter estimation can be conducted using the built-in Markov Chain Monte Carlo (MCMC) method in WinBugs. The student ability and item parameters (from which all tj are derived) can be obtained.

We have applied this novel formulation of PCM to model responses of two items (one is Short Q and the other is Long Q) in the trial run of a test attempted by some 200 students. Short Q has maximum mark equal to 18 and Long Q has maximum mark equal to 20. The outcomes shown in Figure 1 are satisfactory.

All the values of the standard PCM thresholds tj derived from these re-formulated parameters (S, θ, d, c) are provided in Figure 4; together with frequency counts for different response categories.

Summary

In this brief note, we have proposed a novel re-parameterization for PCM in order to handle items with large values of maximum marks. The parameter estimation could be conducted using the freeware, WinBugs. We have applied the re-parameterization to model item responses in some real-life data. The outcomes of the estimations are satisfactory.

Dr. Fung Tze-ho
Manager-Assessment Technology & Research,
Hong Kong Examinations and Assessment Authority

Figure 1. WinBugs parameter estimates and fit statistics.

for (i in 1:N) { # N Students

num.p1[i, 1]<-1
for (j in 1:18){ # An item with max mark = 18
fac11[i,j] <-j*base[1]                        # base[1]:S parameter 
fac12[i,j]<-j*(j-1)*int[1]/2                  # int[1]:q parameter
fac13[i,j]<-j*(j-1)*(j-2)*dev[1]/6            # dev[1]:d parameter
fac14[i,j]<-j*(j-1)*(j-2)*(j-3)*chg.dev[1]/24 # chg.dev[1]:c parameter
num.p1[i, j+1] <- exp(j*lambda[i] - (fac11[i,j] +fac12[i,j] + fac13[i,j] + fac14[i,j] ))}     
den.p1[i] <- sum(num.p1[i,1:19] )
for (j in 1:19){p1[i,j] <- num.p1[i,j]/ den.p1[i] } } # normalization  
for (i in 1:N) 
{r[i, 1] ~ dcat(p1[i, 1:19 ])} # define a categorical distribution       
                               # r[i,1] is the response of student i to the item

Figure 2. WinBugs code for reparameterized PCM with categories 0-18.

for (i in 1:N){lambda[i] ~ dnorm(0, tau.lambda)}

for (j in 1:T){
  base[t] ~ dnorm (mu.Base, tau.Base)
  int[t] ~dnorm(mu.Int, tau.Int )I(0,)
  dev[t]~dnorm(mu.Dev,tau.Dev)
  chg.dev[t]~dnorm(mu.Chg, tau.Chg)
}
   tau.lambda ~ dgamma(0.001, 0.001)   
   mu.Base ~ dnorm(0, 1.E-6)
   tau.Base ~ dgamma(0.001, 0.001)
   mu.Int ~ dnorm(0, 1.E-6)
   tau.Int ~ dgamma(0.001, 0.001)
   mu.Dev ~ dnorm(0, 1.E-6)
   tau.Dev ~ dgamma(0.001, 0.001)
   mu.Chg ~ dnorm(0, 1.E-6)
   tau.Chg ~ dgamma(0.001, 0.001)

Figure 3. WinBugs code for non-informative priors.

Figure 4. PCM thresholds for 19 categories (Short Q) and 21 categories (Long Q).

Note that category 0 is not observed, and nor is category 4 for Short Q. The reparameterized estimation is robust against unobserved categories.

Re-Parameterization of the Partial Credit Model for Estimating Items with Large Values of Maximum Marks, Fung Tze-ho ... Rasch Measurement Transactions, 2011, 24:4, 1301-2

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt244a.htm

Website: www.rasch.org/rmt/contents.htm