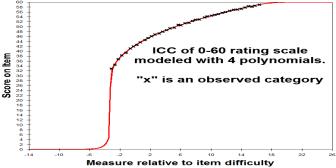
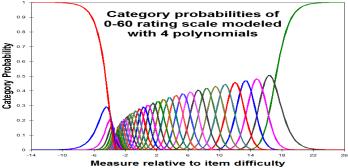
"A reparameterized form of thresholds into their principal components is the method of estimation operationalized in RUMM2030. This notion of principal components is used in the sense of Guttman (1950), who rearranged ordered categories into successive principal components, beginning with the usual linear one. They are analogous to the use of orthogonal polynomials in regression where the independent variable is ordered. The term does NOT refer to the common "principal components analysis" in which a matrix of correlation coefficients is decomposed by analogy to factor analysis."
from www.rummlab.com.au, January, 2011.
As previously described in Guttman Parameterization of a Rating Scale, RMT 17:3, 2003, p. 944, Pender Pedler (1987, amended) constructs the Guttman decomposition of the j = 1 to m Rasch-Andrich thresholds of a rating scale with categories 0,m. He defines a series of k = 1,K orthogonal polynomials in j,
T1(j) = 1
T2(j) = 2 ( j - (m+1)/2 )
T3(j) = 3 ( j - (m+1)/2 )2 - (m2 - 1)/4
T4(j) = 4 ( j - (m+1)/2 )3 - ( j - (m+1)/2 )(3m2 - 7)/5
In general, for polynomial k+1 of threshold j,
Tk+1(j) = [(k+1)/k] ( j - (m+1)/2 )Tk(j) - ([(m2 - (k-1)2)(k2 - 1)]/[4(2k - 1)(2k-3)])Tk-1(j)
So, when {Fj} are the Rasch-Andrich thresholds, and {ck} are the coefficients of the polynomials, estimated from the data by, say, Newton-Raphson iteration,
Fj = sum (ckTk(j)) for k = 1 to K
Note that there is no requirement that all the categories are observed in the data.
Andrich and Luo (2003) use cumulative thresholds, kappa(x), up to threshold x, so that
kappa(x) = - sum(F(j)) for j = 1 to x,
= sum ([sum (ckTk(j)) for k = 1 to K]) for j=1 to x
= sum ((ck / Ak) Uk(x)) for k = 1 to K
where
Uk(x) = Ak.sum(Tk(j)) for j = 1 to x, and Ak is a constant chosen for convenience. c1/A1 is termed the central location, c2/A2 = θ is the dispersion, c3/A3 = η is the skewness, c4/A4= ζ is the kurtosis.
Specifically,
U1(x) = -x, with A1 = -1.
U2(x) = x(m-x), with A2 = -1
U3(x) = x(m-x)(2x-m) with A3 = -2
U4(x) = x(m-x)(5x2-5xm+m2+1) with A4 = -5
However, the utility of the orthogonal polynomials is that each higher polynomial adds to the lower ones. Accordingly, we can stop when we have estimated enough of the polynomials to give a useful definition of the threshold values. This is especially helpful when estimating long rating scales based on small datasets. The example in the Figures models the thresholds with four polynomials. It is based on ratings of Olympic Ice-Skating and is estimated by Winsteps.
John M. Linacre
Andrich, D. & Luo, G. (2003). Conditional Pairwise Estimation in the Rasch Model for Ordered Response Categories using Principal Components. Journal of Applied Measurement, 4(3), 205-221.
Guttman, L. (1950). The principal components of scale analysis. In S.A. Stouffer, L. Guttman, E.A. Suchman, P.F. Lazarsfeld, S.A. Star and J.A. Clausen (Eds.), Measurement and Prediction, pp. 312-361. New York: Wiley
Pedler, P.J. (1987) Accounting for psychometric dependence with a class of latent trait models. Ph.D. dissertation. University of Western Australia.
| |
Guttman Parameterization of Rating Scales - Revisited, J.M. Linacre ... Rasch Measurement Transactions, 2011, 24:4, 1303
| Rasch Publications | ||
|---|---|---|
| Rasch Measurement Transactions (free, online) | Rasch Measurement research papers (free, online) | Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch |
| Applying the Rasch Model 2nd. Ed., Bond & Fox | Best Test Design, Wright & Stone | Rating Scale Analysis, Wright & Masters |
| Introduction to Rasch Measurement, E. Smith & R. Smith | Introduction to Many-Facet Rasch Measurement, Thomas Eckes | Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr. |
| Statistical Analyses for Language Testers, Rita Green | Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar | Journal of Applied Measurement |
|
|
|
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| June 19-21, 2013, Wed.-Fri. | SIS 2013 Conference on Advances in Latent Variables: Methods, Models and Applications, Brescia, Italy, meetings.sis-statistica.org/index.php/sis2013/ALV |
| July 1 - Nov. 30, 2013, Mon.-Sun. | Online Course: Introduction to Rasch Measurement Theory (D. Andrich, RUMM), www.education.uwa.edu.au/ppl/courses |
| July 5 - Aug. 2, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| July 15, 2013, Monday | Application deadline: UIC Educational Research Methodology online graduate certificate program, www.go.uic.edu/OnlineMESA |
| July 22, 2013, Monday | Submission deadline: 2014 AERA Annual Meeting, Philadelphia PA, www.aera.net |
| Aug.1-5, 2013, Thur.-Mon. | TERA-PROMS Annual Meeting, Kaohsiung, Taiwan, tera.education.nsysu.edu.tw |
| Aug. 9 - Sept. 6, 2013, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Aug. 22, 2013, Thursday. | Symposium in honor of Svend Kreiner, Copenhagen, Denmark, biostat.ku.dk/kreinersymposium |
| Sept. 4-6, 2013, Wed.-Fri. | IMEKO TC1-TC7-TC13 Symposium: Measurement Across Physical and Behavioural Sciences, Genoa, Italy, www.imeko-genoa-2013.it |
| Sept. 13 - Oct. 11, 2013, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 18-20, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 23-25, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 26-27, 2013, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Oct. 18 - Nov. 15, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Oct. 20 - Oct. 25, 2013, Sun.-Fri. | International Association for Educational Assessment (IAEA) 39th Annual Conference, Tel Aviv, Israel, www.iaea-2013.com |
| Dec. 11-13, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| March 12-14, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| April 3-7, 2014, Thurs.-Mon. | AERA Annual Meeting, Philadelphia PA, www.aera.net |
| May 14-16, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| May 19-21, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| July 4 - Aug. 1, 2014, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| Aug. 8 - Sept. 5, 2014, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Sept. 10-12, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 12 - Oct. 10, 2014, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 15-17, 2014, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 18-19, 2014, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| The javascript to add "Coming Rasch-related Events" to your webpage is: <script type="text/javascript" src="http://www.rasch.org/events.txt"></script> | |
The URL of this page is www.rasch.org/rmt/rmt244b.htm
Website: www.rasch.org/rmt/contents.htm