Rater-Mediated Domain Response Functions

Rater-mediated assessments are used extensively in a variety of educational contexts (Engelhard, 2002). In evaluating the quality of ratings obtained in these contexts, the idea of rater-mediated operating characteristic functions (rm-OCFs) has not been systematically explored. OCFs can be used to enhance the substantive interpretations of rater behaviors. For example, the substantive interpretation of crossing item response functions (IRFs) is fairly well known (Wright, 1997), and Perkins and Engelhard (2009) have discussed crossing person response functions (PRFs). Similar ideas can be used to develop rater-mediated domain response functions (rm-DRFs), as well as rater-mediated person response functions (rm-PRFs). Just as crossing IRFs or PRFs create differential ordering of item difficulty and person performance, crossing rm-DRFs and rm-PRFs have implications for the substantive interpretation of rater behavior. When rm-DRFs cross, the interpretation of the domains across the latent variable is not invariant above and below the intersection points. This note provides an illustration of crossing rm-DRFs, and demonstrates the substantive interpretation of this situation.

Both Rasch (1960/1980) and Birnbaum (1968) propose operating characteristic functions for dichotomous responses that can be used to model dichotomous ratings. For example, a Rasch model for dichotomous ratings can be written as follows:

[1]

where φnmi is the probability when θn is the judged location of person n on the latent variable (e.g., writing proficiency) by rater m with a severity of λm on domain i with a judged difficulty of δi .

A Birnbaum Model for dichotomous ratings can be written as

[2]

where αi is a scale parameter that varies across domains, and ci is the lower asymptote of the function that represents rater reluctance to assign low ratings to persons (a comparable upper asymptote can also be introduced for rater reluctance to assign high scores).

In the context of rater-mediated assessments, the rm-DRF for a Rasch rater (λR) on domain one (δ1) rated dichotomously (fail/pass) can be written as:

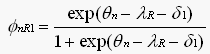[3]

and for a Birnbaum rater (lB):

[4]

The general requirements for invariant measurement are summarized by Engelhard and Perkins (2011), and these requirements can be extended for raters (Wind & Engelhard, 2011):

The measurement of persons must be independent of the particular raters that happen to be used for measuring: Rater-invariant measurement of persons.

Figure 1 illustrates the effects of crossing rm-DRFs for two raters who are rating writing proficiency using three domains: Mechanics (M), Content (C), and Organization (O). Panel A is a Rasch rater with non-crossing DRFs, while Panel B is a Birnbaum rater with crossing DRFs. Panel C shows a substantive interpretation for non-crossing DRFs that produce comparable judged domain difficulties over subgroups of persons. The ordering of the three domains is invariant with the mechanics (M) domain judged easiest and organization (O) domain judged as hardest across the latent variable of writing proficiency. Non-crossing DRFs result in equivalent ordering of domains across subsets of persons, and yields invariant measurement from the Rasch rater.

Panel D shows the substantive interpretation of crossing DRFs based on a Birnbaum rater. The meaning of person performance on domains varies as a function of person subgroup locations on the latent variable of writing proficiency. The Rasch rater interprets the domains in a comparable way over subgroups with domains ordered as M < C < O, while the domain difficulties are variant for the Birnbaum rater. The Birnbaum rater rates the organization (O) domain easiest for persons with low writing proficiency, while organization (O) is rated hardest for persons with high writing proficient.

In practice, model-data fit and the requirements of invariant measurement can be usefully visualized with OCFs. This note highlights the need for researchers to examine differential domain functioning as an additional aspect of model-data fit within the context of rater-mediated assessments. It is recognized that domains may function differently over subgroups of persons (differential domain functioning).

Stefanie A. Wind & George Engelhard, Jr.

Emory University

Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee's ability, Part 5. In F.M. Lord and M.R. Novick (Eds.), Statistical theories of mental test scores. Reading, MA: Addison-Wesley Publishing Company, Inc.

Engelhard, G. (2002). Monitoring raters in performance assessments. In G. Tindal and T. Haladyna (Eds.), Large-scale Assessment Programs for ALL Students: Development, Implementation, and Analysis, (pp. 261-287). Mahwah, NJ: Erlbaum.

Engelhard, G, & Perkins, A.F. (2011). Person response functions and the definition of units in the social sciences. Measurement: Interdisciplinary Research and Perspectives, 9, 40-45.

Perkins, A., & Engelhard, G. (2009). Crossing person response functions. Rasch Measurement Transaction, 23(1), 1183-1184.

Rasch (1960/1980). Probabilistic models for some intelligence and attainment tests. Copenhagen: Danish Institute for Educational Research. (Expanded edition, Chicago: University of Chicago Press, 1980).

Wind, S.A., & Engelhard, G. (2011, July). Evaluating the quality of ratings in writing assessment: Rater agreement, precision, and accuracy. Paper presented at the Pacific Rim Objective Measurement Seminar (PROMS) in Singapore.

Wright, B.D. (1997). A history of social science measurement. Educational Measurement: Issues and Practice, Winter, 33- 45, 52.

Rater Invariant Measurement	Rater Variant Measurement
Panel A: Rasch Rater	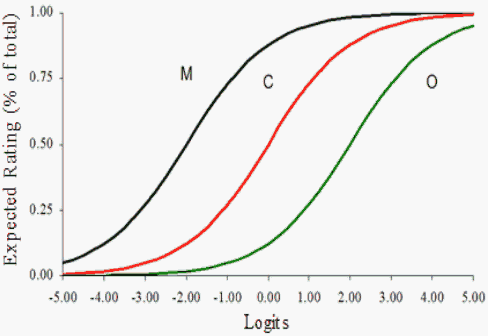Panel B: Birnbaum Rater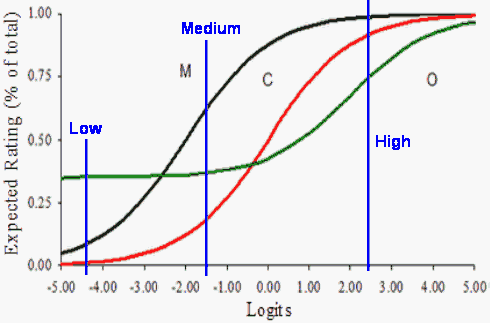
Panel C < Domain       Easy M M M Medium C C C Hard O O O Writing Proficiency Low Medium High	Panel D Domain       Easy O M M Medium M O C Hard C C O Writing Proficiency Low Medium High
Figure 1. Impact of Crossing Rater-Mediated Domain Response Functions. The domains are Mechanics (M), Content (c), and Organization (O).

Rater-Mediated Domain Response Functions, Stefanie A. Wind & George Engelhard, Jr. ... Rasch Measurement Transactions, 2011, 251:2, 1321-2

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt252a.htm

Website: www.rasch.org/rmt/contents.htm