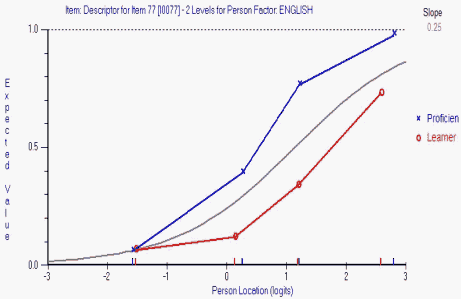
Figure 1. DIF analysis of item 77 of the vocabulary test.
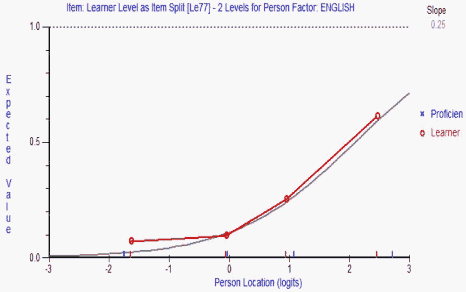
Figure 2. Item "Le77" created by splitting item 77.
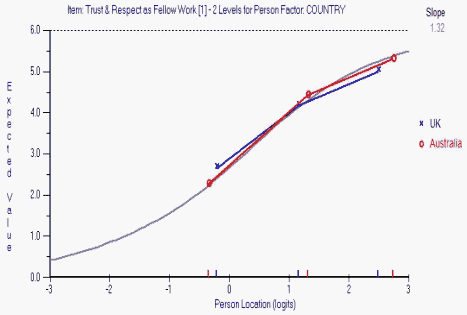
Figure 3. A DIF analysis of the first item of the interpersonal trust questionnaire.
Questions have recently been asked about combining samples from different populations to obtain more precise estimates of Rasch (1960) model parameters. Ceteris paribus, the more data that is available for a given test, the more precise the parameters will be. There can be times, however, when combining different sets of test data may be problematic. Fortunately, a simple way of checking for problems with aggregating data exists. The different samples can be entered into a Rasch analysis as person factors/ facets and the items checked for Differential Item Functioning (DIF).
Application of the Rasch model assumes that parameters are invariant with respect to populations. The presence of DIF voids this assumption. A test in which many items suffer from DIF will produce person ability estimates that are biased. If the DIF is "non-uniform" (e.g., "Sample A's" and "Sample B's" item response functions intersect), then there is a problem and the data should not be combined. In cases of uniform DIF, the item response functions do not intersect, which means that a mathematical transformation could render these curves parallel.
Uniform DIF can be treated in a very powerful way in RUMM2030 by "splitting" the item. This means the Rasch model is used to calculate two different item difficulty parameters for an item affected by uniform DIF - one for Sample A examinees and one for those from Sample B. When RUMM2030 calculates person ability estimates, then depending upon the examinee's classification, one of the two item difficulty estimates is used. For example, for a Sample A examinee, the calculation of that person's ability will use the Rasch item difficulty parameter estimate for Sample A examinees for that item. A simple t test upon the two sets of person ability scale scores (i.e., split and unsplit) can reveal if the mean person ability estimates are statistically significantly different.
I have encountered two recent problems concerning the combination of sample sizes and DIF. The first concerned a vocabulary test consisting of 104 dichotomous items. Initial Rasch calibration was conducted using the RUMM2030 program on a sample of 510 readers. Of these, 288 were classified as an "English Learner" and 222 were "English Proficient". One hundred and seventy three participants were in Grade 4 and 334 were in Grade 3 at the time of test administration.
Overall fit of the Rasch model to the data was poor as many items did not fit the Rasch model. The Total Item Chi Square, which is a sum of individual item chi squares, was 1,137; df = 312, p < .001. The PSI reliability, however, was quite high, being at .96.
The test developers thought that the test suffered from "multidimensionality", but performing a principle components analysis on residual correlations did not reveal any instance of this. DIF was investigated in RUMM2030 by the calculation of Item Response Curves (ICCs) for each person factor for each item. If DIF is not present in the data for an item, there will be no discernable differences between person factor ICCs for that item. Additionally, main effects for the person factor in ANOVA analyses of item residuals will not be statistically significant.
There was no DIF when the person factor involved was Grade. Perhaps not surprisingly, there was a serious and substantial amount of DIF when the English Proficiency/Learning factor was assessed. A DIF analysis of Item 77 is displayed in Figure 1. Two ICCs have been calculated - one for participants who were classed as English Proficient (blue ICC) and one for English Learners (red ICC). If there was no difference between these two groups in performance on this item, then both the red and blue ICCs would both fall on the theoretical grey ICC. In this case they do not, and so therefore this item suffers from DIF.
|
|
Item 77 was amongst those items split. Figure 2 represents the "split" Item 77 for English Learners. The difficulty of Item 77 for English Learners was 2.095. In the original unsplit item, the difficulty was 1.143. Hence the split Item 77 for English Learners, which fits the Rasch model, is a more difficult item for these examinees than the original, which did not fit the Rasch model.
Almost all instances of English Proficiency/Learning DIF in the test were uniform, meaning that most DIF items were split (34 items in total). The test was then recalibrated and all misfitting items, both split and unsplit, were removed from analysis. Forty six items in total were removed. This substantially improved the overall fit of the Rasch model to the data (chi square = 356, df = 276, p < .001). Whilst still statistically significant, the magnitude of the overall chi square statistic was reduced by more than two thirds. The PSI reliability coefficient was .94, which meant that test reliability was only marginally affected by the removal of items. To test the difference between calibrations, person ability estimates from the initial and final calibrations were obtained and a paired samples t-test was conducted. The difference between the means of .315 logit was statistically significant (t(506) = 23.82, p < .001, one tailed). Hence the DIF in the initial calibration caused person ability estimates to be biased by an average of almost one third of a logit.
Thus "multidimensionality" was not the culprit for poor fit of the Rasch model. It was the test developers' decision to administer the test to samples of examinees from two very different populations - those just beginning to learn English and those who were proficient in it. Nonetheless, item splitting salvaged the test calibration.
The other problem was something quite different. An academic colleague combined two samples of managers - 107 from the U.K. and 85 from Australia - to analyze a questionnaire of interpersonal trust. In response to a paper written on the project, a reviewer stated that "... combining the UK and Australian samples of sales managers into one dataset generates additional confounding ... country-level effects will potentially bias the estimates and this poses a serious problem". Testing items for DIF was a means of being able to test the reviewer's conjecture.
Figure 3 displays the UK and Australian sample ICCs for the first test item, which read "Most people, even those who aren't close friends of the marketing manager, trust and respect him/her as a fellow worker."
Like the first item in Figure 3, no other item in the test suffered from DIF. Moreover, the test was reliable (Cronbach's alpha = .94). The combining of samples from different nationalities was therefore justified as this caused no discernable bias in the Rasch parameter estimates.
Andrew Kyngdon, MetaMetrics, Inc.
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. Copenhagen: Danish Institute for Educational Research.
RUMM Laboratory Pty Ltd. (2009). RUMM2030™ [Computer software]. Perth, Australia: Author.
Is Combining Samples Productive? A Quick Check via Tests of DIF, Andrew Kyngdon ... Rasch Measurement Transactions, 2011, 251:2, 1324-5
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt252b.htm
Website: www.rasch.org/rmt/contents.htm