The Effects of Local Item Dependence on Estimates of Ability in the Rasch Model

One of the most crucial assumptions of psychometric theory is that the relationship between items is accountable to a specific latent trait. However, a major issue in psychometrics is what happens when items continue to relate with each other, after accounting for their contribution to the latent trait. In the context of the Rasch model, this relationship is termed Local Item Dependence (LID), and represents a prerequisite and assumption of the model. Violation of this assumption states that there is still some covariation between items, although the relationship of each item to the latent trait has been accounted for. The issue of local item dependency relates strongly to the issue of unidimensionality (as that covariation could be easily explained by the presence of a second factor), but could also relate to other sources of measurement error (e.g., situational such as fatigue or rater effects). Furthermore, violation of this assumption has major implications regarding the validity of estimates (e.g., on discrimination) of the Rasch model (Tuerlinckx & de Boeck, 2001; Yen, 1993). The assumption has been described in mathematical form by Tuerlinckx and de Boeck (2001):

This implies that the association between items (adjacent or not) should be zero. In that case, the true latent score of a person should equal the observed estimate. The purpose of the present paper was to evaluate the effects of local item dependence on the ability parameters of a spatial test involving a series of Chinese tangrams (i.e., puzzle). Participants were 94 university students with a major in psychology who completed the Chinese tangrams in response for extra credit. The specific hypothesis posited was that item difficulties of the Puzzle would be overestimated in the presence of local item dependence. The present illustration involves the manipulation of local item dependency on two puzzles only, for simplicity. Prerequisite analyses involve evaluation of the presence of local dependency. Within the framework of Hierarchical General Linear Modeling (HGLM), and as recommended by Johnson and Raudenbush (2006), this evaluation involved examination of the within-person variance σ² under the Bernoulli model (with the expectation being that σ² = 1). Applications of both restricted and full maximum likelihood procedures indicated that σ² was significantly lower compared to the expectation of the Bernoulli model (actual value of σ² was equal to 0.52, after rounding for both solutions), suggesting the presence of local item dependencies.

To evaluate the effects of local item dependence, a Rasch model was initially estimated using the Bernoulli function in Hierarchical Generalized Linear Modeling (HGLM). As Kamata (2002) demonstrated the following two-level HGLM model shown below is equivalent to the Rasch model:

Level-1 (Bernoulli) Model:

Level-2 model expressing person estimates:

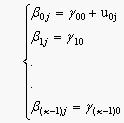
The term p_ij reflects the probability that person j will answer item i correctly. The term X_ij describes the ith dummy variable for participant j. Last, the term βoj reflects the intercept of the model (as in dummy variable regression) and β_1j through βkj the coefficients of puzzle items X1 through Xk. The random term u_0j is the error around the intercept, which is expected to be normally distributed (with a mean of zero and variance equal to τ). When the above two-level model is applied to the data of person j for a specific item i, the probability of that person responding correctly to item i is expressed as:

The following two level HGLM model was tested in order to estimate item abilities of the Rasch model:

Level 1

Prob (Response_ij = 1|βj = φ_ij

Log [φ_ij / 1 - φ_ij) = η_ij

η_ij = β_0j + β_1j (Puzzle1) + β_2j (Puzzle2) + β_3j (Puzzle3) + β_4j (Puzzle4) + r_ij

Level 2

β_0j = γ₀₀ + u_0j
β_1j = γ₁₀
β_2j = γ₂₀
β_3j = γ₃₀
β_4j = γ₄₀

As shown above, only four puzzles are included in the model with the 5th one being represented by the intercept. The above model was compared to the model below in order to account for the presence of local dependence between puzzles 4 and 5. However, first there is a description of the interaction model used to account for the interaction between the two items. The model has been referred to as the constant interaction model (Tuerlinckx & de Boeck, 2001) because the interaction is presumably equal in magnitude across all participants. It is expressed in the following function:

The above model applies to two binary items denoted by the numbers 1 and 2. The responses to the items are seen as a realization of a bivariate random variable (X1, X2) and for a particular realization (x1,x2) the model is as shown above. The term β12 expresses the interaction between puzzles 4 and 5.

The estimated HGLM model employed to account for the above dependency was the following:

Level 1

Prob (Response_ij = 1|βj = φ_ij

Log [φ_ij / 1 - φ_ij) = η_ij

η_ij = β_0j + β_1j (Puzzle1) + β_2j (Puzzle2) + β_3j (Puzzle3) + β_4j (Puzzle4) + β_5j (Puzzle5) + r_ij

Level 2

β_0j = γ₀₀ + u_0j
β_1j = γ₁₀
β_2j = γ₂₀
β_3j = γ₃₀
β_4j = γ₄₀
β_5j = γ₅₀

The difference between the two HGLM models is on their intercepts. In the Rasch model the intercept expressed the last item (as in dummy regression) whereas in the conditional independence assumption model the intercept represented the interaction (local dependency) between puzzle 4 and 5.

Figure 1 shows the effects of local item dependence on the difficulty levels of puzzle 4 and 5. It is obvious from item 5, the after controlling for local item dependency (i.e., its relation with item 4), the estimated difficulty of the item went down. This finding agrees with the theses of Douglas, Kim, Habing, and Gao (1998) who stated that the difficulty of the item is affected by the interacting item (5 in our case) and not the first item of the interaction (item 4). This finding also agrees with the suggestions of Thissen, Steinberg, and Mooney (1989) who stated that when local item dependencies are positive, and are not accounted for, theta values are greatly overestimated (Yen, 1993 reported the same finding, attributed it to the underestimation of the standard errors of measurement). Tuerlinckx and de Boeck (2001), put it more intuitively: "If two items interact positively, they provide less information than two independent items." (p. 186). That is, if they are treated as being independent their information regarding the latent trait is greatly overestimated. This effect is shown on the puzzle's total response functions when accounting for or ignoring local dependence (Figure 2). The curves on Figure 2 show that at higher levels of ability (i.e., last two puzzles) the two forms become more and more different. Similar information is provided by the Test Information Functions (TIFs) of the two forms, with differences being observed at higher levels of ability (theta).

Summary

The purpose of the present paper was to evaluate the effects of local item dependence on the ability parameters of a series of puzzle. Results indicated that the effects of local independence are substantial and likely inflate the ability estimates of items at a given scale. Thus, the presence of LID seriously distorts the qualities of the items. Ideally, researchers should examine and control for the presence of LID. In HGLM, one can allow for under-dispersion in order to correct for local item dependency.

In the Rasch model one can estimate the likelihood ratio test, but as Tuerlinckx and de Boeck (2001) reported the test has little power and can reveal either large numbers of interacting items or extreme interactions (thus, it leaves several cases of LID undetected). It is concluded that LID represents a serious psychometric nuisance and should be evaluated at all times. It is suggested that hybrid Rasch models should be implemented to account for its deleterious effects on the quality of the items.

Georgios D. Sideridis
University of Crete

Douglas, J., Kim, H., Habing, B., Gao, F. (1998). Investigating local dependence with conditional covariance functions. Journal of Educational and Behavioral Statistics, 23, 129-151.

Johnson, C., & Raudenbush, S. (2006). A repeated measures multilevel Rasch model with application to self-reported criminal behavior. In C. Bergeman, & S. Boker, (Eds.), Methodological issues in aging research. Mahwah, NJ: Lawrence.

Kamata, A. (2002, April). Procedure to perform item response analysis by hierarchical generalized linear model. Paper presented at the annual meeting of the American Educational Research Association, New Orleans.

Thissen, D., Steinberg, L., & Mooney, J. A. (1989). Trace lines for testlets: A use of multiple-categorical-response models. Journal of Educational Measurement, 26, 247-260.

Tuerlinckx, F., & De Boeck, P. (2001). The effect of ignoring item interactions on the estimated discrimination parameters in item response theory. Psychological Methods, 6, 181-195.

Yen, W. M. (1993). Scaling performance assessments: Strategies for managing local item dependence. Journal of Educational Measurement, 30, 187-213.

The Effects of Local Item Dependence on Estimates of Ability in the Rasch Model, Georgios D. Sideridis ... Rasch Measurement Transactions, 2011, 25:3, 1334-6

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt253d.htm

Website: www.rasch.org/rmt/contents.htm