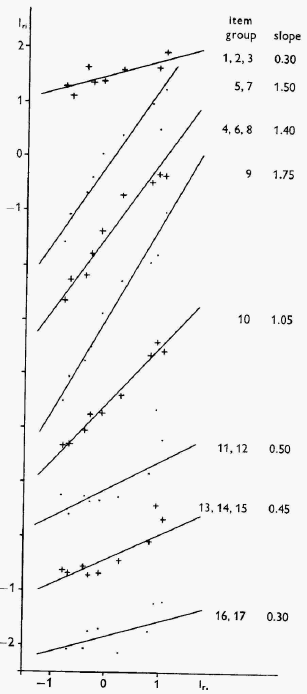
Figure 14. Subtest F of BPP. lri plotted against lr. for each group of items. From Rasch (1960) "Probabilistic Models for Some Intelligence and Attainment Tests".
Georg Rasch didn’t expect all kinds of items to fit a Rasch model in all kinds of frames of reference, so he was always extremely careful about testing the items to see whether there was something wrong with the way they had been constructed or with the theory underlying the items. He was in fact an absolute fundamentalist when it came to model checking not only for the Rasch model, but for all kinds of statistical models.
|
Figure 14. Subtest F of BPP. lri plotted against lr. for each group of items. From Rasch (1960) "Probabilistic Models for Some Intelligence and Attainment Tests". |
Graphical techniques were very important to Rasch. He had a principle saying (in Danish) that you should "tegne" before you "regne" (meaning "plots" before "calculations") and he had a lot of students (including Peter Allerup) doing the plots for him. He would never draw the ICC curves as we do today. Rasch plotted the logistic values of the probabilities against estimates of person parameters (or similar but more complicated functions of the item parameters against the total scores) because it is much easier to assess systematic departures from straight lines than departures from logistic curves (See Figure from Rasch, 1960).
In addition to these plots he would, of course, also use numerical tests and he would always insist that these calculations should be made relative to the conditional distribution of item responses given the total score to make sure that he had separated his inference on items from the persons.
You can find some of this in his 1960 book, but far from all. We know that he at some point worked on a sequel to the book that he never finished. When we celebrated his centenary in 2001 we published a collection of his unpublished papers and notes. (You can find this collection at www.rasch.org/memos.htm). Among these papers we included a chapter on "Estimation of Parameters and Control of the Model for Two response Categories" where he describes five different methods including a test for the hypothesis that the item discrimination is the same for all items and including much of the theory of conditional inference that Erling B. Andersen worked on and published during the 70’es. It is quite interesting reading so take a look at it. You can find it at www.rasch.org/memo196y.pdf.
Rasch’s view on item fit analyses were that evidence against the item means that it should be either revised
(if at all possible) or removed. That goes both for items where item discrimination is too weak and items where
discrimination is too strong (Infits and/or Outfits that are smaller than 1). That is also my point of view,
but the interpretation of the lack of fit of the item is very different for items that do not discriminate and items
with too strong discrimination. In the first case I would suspect inept item writing or multidimensionality.
In the second case I would always look for evidence of local response dependence (LD) because I know that positive
local dependence has the effect that the item discrimination of the items look stronger than expected by the Rasch model.
It is my experience this is the case in many of the analyses where I find evidence of too strong discrimination.
You can find one such example in
Kreiner S (2011) A Note on Item-Restscore Association in Rasch models. Applied Psychological Measurement, 35, 557-561
where the local dependence is a consequence of inept item writing in the sense that items are phrased in such a way that local dependence is unavoidable.
Svend Kreiner
University of Copenhagen
Denmark
Georg Rasch and Item Fit, S. Kreiner, Rasch Measurement Transactions, 2012, 26:1, 1354
| Rasch Publications | ||
|---|---|---|
| Rasch Measurement Transactions (free, online) | Rasch Measurement research papers (free, online) | Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch |
| Applying the Rasch Model 2nd. Ed., Bond & Fox | Best Test Design, Wright & Stone | Rating Scale Analysis, Wright & Masters |
| Introduction to Rasch Measurement, E. Smith & R. Smith | Introduction to Many-Facet Rasch Measurement, Thomas Eckes | Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr. |
| Statistical Analyses for Language Testers, Rita Green | Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar | Journal of Applied Measurement |
|
|
|
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| June 19-21, 2013, Wed.-Fri. | SIS 2013 Conference on Advances in Latent Variables: Methods, Models and Applications, Brescia, Italy, meetings.sis-statistica.org/index.php/sis2013/ALV |
| July 1 - Nov. 30, 2013, Mon.-Sun. | Online Course: Introduction to Rasch Measurement Theory (D. Andrich, RUMM), www.education.uwa.edu.au/ppl/courses |
| July 5 - Aug. 2, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| July 15, 2013, Monday | Application deadline: UIC Educational Research Methodology online graduate certificate program, www.go.uic.edu/OnlineMESA |
| July 22, 2013, Monday | Submission deadline: 2014 AERA Annual Meeting, Philadelphia PA, www.aera.net |
| Aug.1-5, 2013, Thur.-Mon. | TERA-PROMS Annual Meeting, Kaohsiung, Taiwan, tera.education.nsysu.edu.tw |
| Aug. 9 - Sept. 6, 2013, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Aug. 22, 2013, Thursday. | Symposium in honor of Svend Kreiner, Copenhagen, Denmark, biostat.ku.dk/kreinersymposium |
| Sept. 4-6, 2013, Wed.-Fri. | IMEKO TC1-TC7-TC13 Symposium: Measurement Across Physical and Behavioural Sciences, Genoa, Italy, www.imeko-genoa-2013.it |
| Sept. 13 - Oct. 11, 2013, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 18-20, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 23-25, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 26-27, 2013, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Oct. 18 - Nov. 15, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Oct. 20 - Oct. 25, 2013, Sun.-Fri. | International Association for Educational Assessment (IAEA) 39th Annual Conference, Tel Aviv, Israel, www.iaea-2013.com |
| Dec. 11-13, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| March 12-14, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| April 3-7, 2014, Thurs.-Mon. | AERA Annual Meeting, Philadelphia PA, www.aera.net |
| May 14-16, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| May 19-21, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| July 4 - Aug. 1, 2014, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| Aug. 8 - Sept. 5, 2014, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Sept. 10-12, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 12 - Oct. 10, 2014, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 15-17, 2014, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 18-19, 2014, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| The javascript to add "Coming Rasch-related Events" to your webpage is: <script type="text/javascript" src="http://www.rasch.org/events.txt"></script> | |
The URL of this page is www.rasch.org/rmt/rmt261b.htm
Website: www.rasch.org/rmt/contents.htm