A Comment on the H^T Person Fit Statistic

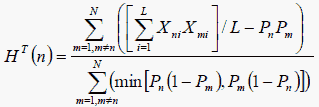
The non-parametric H^T fit statistic (Sijtsma, 1986) is a transposed formulation of Loevinger's H scalability coefficient for items. It is evaluated by Karabatsos (2003). He reports "Overall, the H^T statistic is best [of 36 person fit statistics] in identifying aberrant test respondents. It is also among the best in detecting each of the five different types of aberrant-responding examinees, and in detecting such examinees in each of the short, medium, and long test conditions."

H^T is defined for the rows (persons) of a complete rectangular dichotomous dataset.. Let us focus on person n in a dataset which has L items and N persons. Then, following Karabatsos (2003),

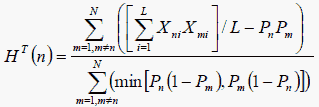
where X_ni is the scored (0,1) response of person n to item i, and P_n = S_n/L where S_n is the raw score of person n, and similarly for person m.

According to Karabatsos (2003), "the critical values H^T = .22 best identify aberrant-responding examinees." In my own informal analyses, the correlation between H^T and the Rasch Infit mean-square was about -0.9, but I was unable to identify a unique Infit mean-square value corresponding to H^T = .22. Since Sijtsma and Molenaar (2002) report 0.3 to be a critical value for coefficient H, a small simulation study may be required to determine the critical value of H^T for a specific empirical dataset.

John Michael Linacre,/p>

Karabatsos, G. (2003). Comparing the aberrant response detection performance of thirty-six person-fit statistics. Applied Measurement in Education, 16(4), 277-298.

Sijtsma, K. (1986). A coefficient of deviant response patterns. Kwantitative Methoden, 7, 131-145.

Sijtsma K,, Molenaar I.W. (2002). Introduction to Nonparametric Item Response Theory. Thousand Oaks, CA: Sage.

A Comment on the H^T Person Fit Statistic, J.M. Linacre, Rasch Measurement Transactions, 2012, 26:1, 1358

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt261f.htm

Website: www.rasch.org/rmt/contents.htm