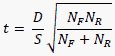
Differential Item Functioning DIF Sample Size Nomogram

Differential Item Functioning (DIF) compares the difficulty of an item for a person sample of interest, the Focal Group (F), with the difficulty of the item for another group, the Reference Group (R). As we plan to investigate DIF, several questions arise:

• 1) What difference between the two item difficulties, i.e., what DIF size, is large enough to have substantive consequences? If we lack better information about the situation, we may choose the DIF size specified by Educational Testing Service which is 1 Delta δ unit = 0.426 logits (see RMT 20:3 p. 1070), rounded up to 0.5 logits for sample-size purposes.

• 2) What difference between item difficulties is unlikely to be merely a chance result, i.e., when is the DIF size statistically significant? We usually choose the conventional statistical significance level, p ≤ .05 (Fisher, 1926).

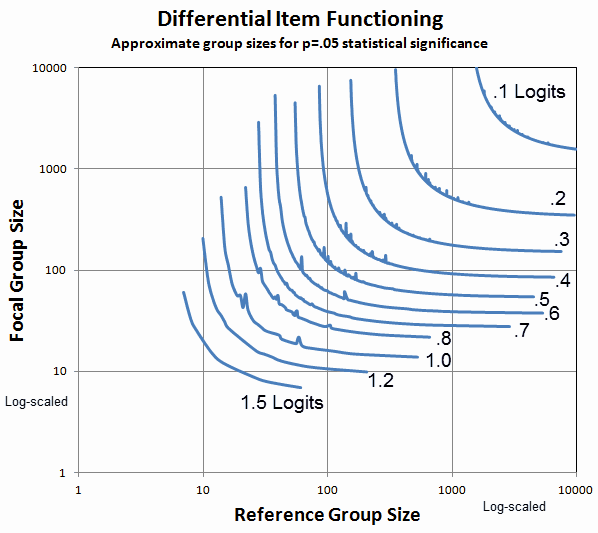
• 3) How many members of the Focal and Reference Groups are required for the DIF size specified in (1) to meet the DIF significance criterion specified in (2)? What samples sizes are required? This nomogram provides a guide.

The nomogram is based on a Student's t-statistic with two independent groups of different sizes, NF and NR, but equal standard deviations, S. The t-statistic of the DIF size, D, is

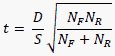
Group size values are chosen such that the two-sided probability of observing t or greater is p = .05 for the specified DIF size, D. The standard deviation, S, is chosen at a reasonable value, 1.88 logits, based on inspection of empirical data.

Example: if our Focal group size is 100, and our Reference group size is 1000, then the DIF size will need to be 0.4 logits or more to be statistically significant.

John Michael Linacre

Fisher R.A. (1926). The arrangement of field experiments. Journal of the Ministry of Agriculture, 33: 504.

Tristan, A. (2006). An adjustment for sample size in DIF analysis. Rasch Measurement Transactions, 20:3, p. 1070-71.

Revised 11 November 2015, with acknowledgement to Siddhi Pittayachawan.

Linacre J.M. (2013) Differential Item Functioning DIF Sample Size Nomogram, Rasch Measurement Transactions, 26:4 p. 1391

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt264a.htm

Website: www.rasch.org/rmt/contents.htm