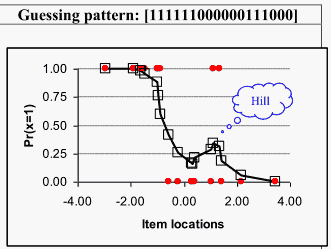
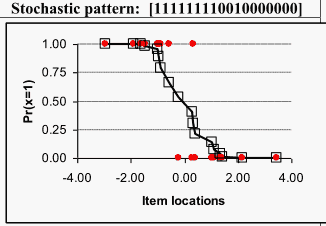
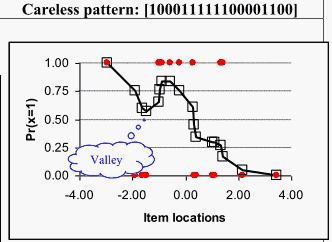
Figure 1: Person response functions.
Note. The red points represent the observed responses (xi), and the boxes represent the smoothed responses (si). Items are ordered from easy to hard.
|
Figure 1: Person response functions. Note. The red points represent the observed responses (xi), and the boxes represent the smoothed responses (si). Items are ordered from easy to hard. |
Person response functions (PRFs) offer an approach for providing additional information when aberrant person response patterns are encountered. PRFs can be based on parametric IRT models, such as the Rasch model. Nonparametric PRFs offer another way to estimate PRFs that may reveal unusual aspects of a person's responses to a set of items including non-monotonic relationships between item locations and person responses. A promising estimator for smoothing functions called "hanning" has been suggested by Tukey (1977) based on a method proposed by von Hann (1903). This estimator provides a nonparametric approach for modeling a functional relationship between calibrated item difficulties and person responses.
A simple version of this algorithm recommended by Velleman and Hoaglin (1981) is given by
si = (yi-1 + 2yi + yi-1) / 4 [1]
where yi is replaced by si. In the context of person response functions, the sequence of values that define the x-axis are based on item calibrations, and the values on the y-axis to be smoothed by Equation 1 are the dichotomous person responses (where yi = 0,1 with 0 representing an incorrect response and 1 representing a correct response to item i by a person). These smoothed values offer a promising approach for illuminating various aberrant and unexpected responses through graphical displays. In essence, the first iteration reflects empirical proportions (weighted) of number correct responses for subsets of four items. The smooth values can continue to be smoothed in an iterative fashion.
In order to illustrate the hanning of person response patterns, item calibrations from Engelhard et al. (in press) are used. The usage items (N=18) for assessing writing from the 2009 administration of the SAT writing assessment define the latent variable (x-axis). Nine iterations of Equation 1 are used to yield the smoothed values in this study.
Figure 1 presents three possible response patterns for students with average scores (50% correct): a guessing pattern, a stochastic pattern, and a careless pattern. The guessing pattern shows a distinctive "hill" reflecting unexpected success on harder items. The careless pattern shows a "valley" with unexpected failure on easier items. The stochastic pattern shows responses that would exhibit good fit to a parametric PRF. PRFs can display hills and valleys in response patterns that may provide the basis for proposing substantive hypotheses, such as guessing and careless behaviors, that merit future study.
In summary, person response functions provide graphical displays that convey information about idiographic aspects of each person's response pattern. Standard errors of measurement for estimated person scores are not sufficient for reflecting the uncertainty in each person's response pattern. Person fit indices are helpful, but multiple response patterns can yield comparable misfit values for most person fit statistics. Person fit statistics do not provide unequivocal interpretations of response patterns without additional inquiry. As pointed out by Tukey (1977),
a basic problem about any body of data is to make it more easily and effectively handleable [and] anything that makes a simple description possible makes the description more easily handleable [and] anything that looks below the previously described surface make the description more effective (p. v)
Hanning PRFs is an approach for making person scores more "handleable" by displaying the potential functional relationships that may explain individual response patterns.
George Engelhard, Jr.
Emory University
References
Engelhard, G., Kobrin, J., Wind, S.A., & Chajewski, M. (in press). Differential item and person functioning in large-scale writing assessments within the context of the SAT Reasoning Test. College Board Research Report.
Tukey, J.W. (1977). Exploratory data analysis. Reading, MA: Addison-Wesley Publishing Company.
Velleman, P.F., & Hoaglin, D.C. (1981). Applications, basics, and computing of exploratory data analysis. Boston, MA: Duxbury Press.
von Hann, J. (1903). Handbook of climatology. New York: The Macmillan Company.
George Engelhard, Jr. (2013) Hanning (Smoothing) of Person Response Functions. Rasch Measurement Transactions, 26:4 p. 1392-3
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt264b.htm
Website: www.rasch.org/rmt/contents.htm