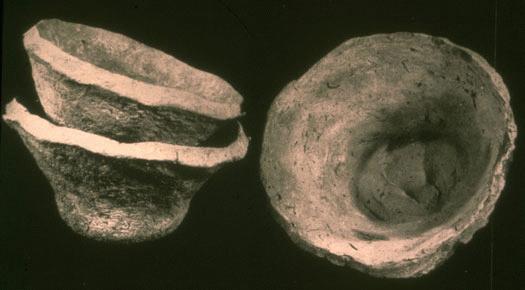
unit-sized ration bowls: The Joukowsky Institute of Archaeology
Ben Wright sometimes used the analogy of sticks when discussing measures. Best Test Design (Wright & Stone, 1979) was to begin with such a discussion, but we changed to another analogy - the arrow. Later, Measurement Essentials (Wright & Stone, 1996) included a figure encompassed by sticks. The sticks have since come to serve as a primitive measure analogy useful to illustrate constructing variables. This urgrund [very basis] of sticks becomes a foundation to making measures. The sequence is as follows:
The analogy of sticks provokes the construction of spelling items, math problems, indicants of depression, fear, anxiety, shame, etc. This approach is further illustrated and confirmed by observing the decreasing lengths of marimba key-length for unit scale differences in well-tempered pitch, likewise for varying string length observed on the harp or a concert grand piano, and the decreasing lengths of organ pipes. It is further manifested by experiments dating back at least to the Greeks, if not earlier, who used the monochord as the basis for the study of "music" (more correctly the fundamentals of today's acoustics) comprising one science in the medieval quadrivium [arithmetic, geometry, music, and cosmology].
 unit-sized ration bowls: The Joukowsky Institute of Archaeology |
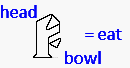 Sumerian pictograph: eat |
Unique aspects for developing measures were employed much earlier according to archeological findings. One example comes from the Early High Period (c. 3200-2800 BCE) of the ancient Middle East documented by Nissen (1988) who identified a "unit bowl" used for dispensing the daily food ration across the entire Babylonian Empire. The proliferation of these unit bowls throughout the empire testify to a standard economic unit identifiable not just by its unit volume, but more so by its unique construction to designate its singular purpose, and keep it distinct from all other pottery. Furthermore, the pictograph of this bowl together with a head indicates "to eat."
An orderly arrangement of sticks can be associated with the axioms of quantity suggested by Höelder (1901) as given by Nagel (1931):
| Nagel's axioms | Stick order as numbered above |
|---|---|
| 1. Either a > b, or a < b, or a = b. | 1, 2, 3, 4 |
| 2. If a >b, and b > c, then a > c. | 5 |
| 3. For every a there is an a' such that a = a'. | 2, 3, 4 |
| 4. If a > b, and b = b' , then a > b'. | 2, 3, 4 |
| 5. If a = b, then b = a. | 1, 2, 3, 4 |
| 6. For every a there is a b such that a > b (within limits). | 2, 3, 4 |
| 7. For every a and b there is a c such that c = a + b. | 8, 9 |
| 8. a + b > a'. | 8, 9 |
| 9. a + b = a' + b'. | 2, 3, 4 |
| 10. a + b = b + a. | 1 |
| 11. (a + b) + c = a + (b + c). | 8, 9 |
| 12. If a < b, there is a number n such that na > b (also within limits). | 8, 9 |
These axioms can be somewhat aligned to the sequence of sticks as indicated in the column to the right of the axioms. The association need not correspond perfectly to substantiate the value of the "sticks" analogy in demonstrating how useful a primitive form of determining measures can be in producing a model for measuring. The alignment is not nearly as important as the fact that the sticks and axioms are both orderly constructions illustrating their importance in systematic fabrication. "All measurement rests upon having a qualitative ordering of the set of objects," write Luce and Narens (1981, p. 215). Order by comparison is essential to any construction.
We should not slight nor dismiss the role of simple strategies for conveying sophisticated processes. Once considered the domain of analysis, elementary school students are now exposed to previously advanced concepts such as the commutative, associative, distributive and transitive processes. Leopold Kronecker is said to have attributed creation of the integers to God, and all other mathematics to creation by man. We are a fabricating people.
Michell (2003, p. 300) provides some similar conditions which "characterise (sic) length as a continuous quantitative variable:
While these conditions suggest "length" in their specifications, the sticks "produce" length! The difference is considerable inasmuch as specification denotes a retrospective mathematical process by means of axioms, whereas the sticks fabricate length as a measure appearing before our eyes. The value of axiomatic specification is to provide a succinct, internally consistent process of logical steps, but Guttman (1971, p. 346) wrote, "Even in mathematics, axiomatization is an intermediate developmental stage; one must first have some idea of some body of inter-relationships for which the axiomatization may be fruitful." The ideals of exactness and rigor in mathematics are the product of time and refinement. The order of sticks manufactures length from operations that evolved early and developmentally; the same process by which any variable might be initially produced. Instrument refinement requires theory, continuous quality control, validation, etc., but that is another story.
 |
A sense of cold and heat is crudely qualitative. We feel "hot" or "cold." Measures of temperature are made quantitative by fashioning a graduated tube constructed of glass together with mercury contained in a vacuum. This approach follows from numerous experiments using water, alcohol, etc. The instrumentation improved because the goal remained constant. Today it is a uniform association between the expansion of mercury and a measure of temperature. The sensations of cold and heat are derived from the human organism while temperature is manufactured analogously by an instrument -- a thermometer; a process little different from using sticks. We "sense" the temperature according to what thermometer scale we most commonly employ. Wittgenstein (1958, sec. 508) writes, "I am not used to measuring temperatures on the Fahrenheit scale. Hence, such a measure of temperature 'says' nothing to me." F-70 means pleasant and F-32 means freezing to those who are familiar with the scale. The matter rests upon an analogy, and the associations that are important for interpreting a measure. A NexTemp® (2004) thermometer is strikingly similar to the sticks analogy, but uses "chemical cavities" instead of sticks to "box in" one's temperature.
The sensation of cold and heat is experienced and crudely categorized. Temperature is constructed by employing comparison and order. A sensation usually lacks clear lines of demarcation further hampered by the "swamp of language." Thermometers employ a sequence of units (numbered) which, when correctly constructed and employed, produce an unambiguous result. A sensation seeks clarity as though residing in a fog, while a working thermometer produces a consistent, useful value. When Chang (2004) selected Inventing Temperature as the title of his book he proclaimed the essence of measuring. Measuring is invention, the process of variable construction, and that inventive process is never ending.
There is reality, and there is one's idealized goal. We might ponder G. H. Hardy's remark that "nothing practical" would occur in his Course of Pure Mathematics (1908), except "constructing" a world of mathematics.
We dwell in a fabricated land straddling two realms - the real and the ideal.
Mark Stone and Jack Stenner
References
Chang, H. (2004). Inventing temperature. New York: Oxford University Press.
Guttman, L. (1971). Measurement as structural theory. Psychometrica, 36(4), 329-347.
Hardy, G. H. (1908). Course in pure mathematics. London: Cambridge University Press.
Höelder, O. (1901) Die Axiome der Quantität und die Lehre von Mass. Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse, 53, 1-46.
Luce, H. D. & Narens, L. Axiomatic measurement theory. SIAM-AMS Proceedings, 13, 213-235.
Michell, J. (2003). Measurement: A beginner's guide. Journal of Applied Measurement 4(4), 298-308.
Nagel, E. (1931). Measurement, Erkenntnis, Band 2, 313-333.
NexTemp® (2004). Medical Indicators, Inc. @medicalindicators.com.
Nissen, H. (1988). Early history of the ancient near east. Chicago: The University of Chicago Press.
Wittgenstein, L. (1958). Philosophical investigations. New York: Macmillan.
Wright, B. & Stone, M. (1979). Best test design. Chicago: MESA
Wright, B. & Stone, M. (1996). Measurement essentials. Wide Range. Available at www.rasch.org/rasch.htm
Concatenating Sticks and Measurement Axioms, Stone M.H, & Stenner A.J. … Rasch Measurement Transactions, 2013, 26:4 p. 1395-7
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt264e.htm
Website: www.rasch.org/rmt/contents.htm