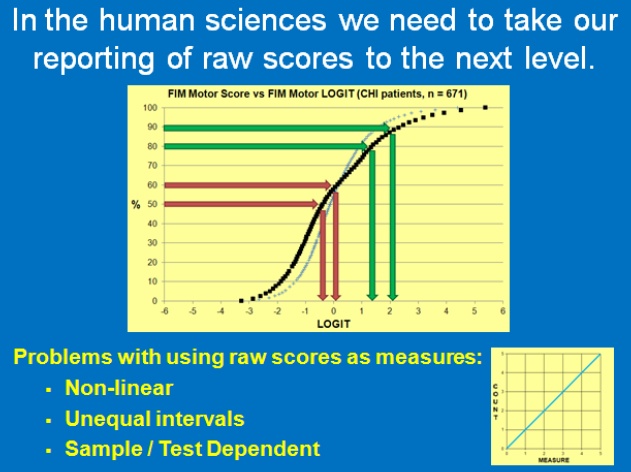
Figure 1: Summary slide showing FIM Motor Raw Scores versus FIM Motor LOGITs (Closed Head Injury patients, n = 671)
This is a short exercise designed to get people thinking about the difference between counting and measuring. This exercise utilizes the fact that balloons are highly similar manufactured products. But they can be manipulated by the trainer in terms of their number, size and color. Helium filled balloons are also easy to obtain and visually engaging. They are large enough for students to see in any classroom. This presentation is dedicated to Dr. Benjamin D. Wright - psychological measurement hero! It starts with the replication of some famous graphs by Dr. Wright (Wright 1993, Wright 1997).
"As researchers and clinicians in the human sciences we need to take our reporting of raw scores to the next level. Raw scores have three fundamental problems when they are used as measures. They are: non-linear, based on unequal intervals, and sample or test dependent.
The graph in Figure 1 shows the relationship between these raw score percentages with their corresponding linear measure. It shows:
 Figure 1: Summary slide showing FIM Motor Raw Scores versus FIM Motor LOGITs (Closed Head Injury patients, n = 671) |
"I would now like to demonstrate these points with some simple exercises. They highlight the difference between counting and measuring, and introduce the concept of the number line."
The correct answers to my questions are in bold.
DEMONSTRATING NON-LINEARITY
Show 3 helium filled balloons of the same size and color (NB: each balloon is tied to a ribbon). Holding the three balloons in one hand, ask the following question:
 |
"How many balloons am I holding?" 3
Now release some of the helium from one of the three balloons. Hold them up again and ask:
 |
"How many balloons am I holding now?" 3
Then ask "Which set of balloons would you prefer to have?" The first set
"Can you see the difference? In one set of balloons we are counting and in the other set we are measuring." This example can be seen on the number line below:
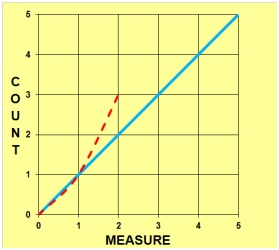 |
This example shows the difference between counting and measuring, and the need to have a one to one correspondence between our counts and our measures.
DEMONSTRATING UNEQUAL INTERVALS
Get a set of 3 balloons, each tied to a weight. Use one large balloon followed by one small balloon and then one large balloon. Place them on the left hand side of the room. Space them about one meter apart.
Then get another set of 3 balloons each tied to a weight. This time the balloons are of equal size. Place them on the right hand side of the room. Space them about one meter apart.
 |
Stand behind the balloons on the left hand side of the room. Start with the balloon on your right.
"I start from here (Step across the next two balloons) and move to here, taking the balloons as I go."
Now go to the example on the right hand side of the room. Stand behind the balloons and start with the balloon on your right.
 |
"I start from here (Step across the next two balloons) and move to here, taking the balloons as I go."
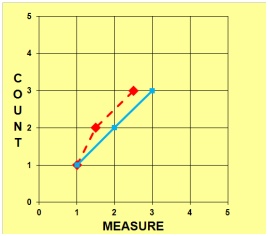
"Now, in which example have I made the most improvement or gain?" The second example
This example can be seen on the number line below:
 |
"Now imagine that I painted the numbers one, two and three on the front of these balloons. Would this make any difference to your answer?"
(This comment brings up the issue of using numbers as object labels or identifiers.)
"Here is another example."
Show a set of 3 balloons: one small, one medium and one large.
 |
"Here the balloons are in size order. The last balloon is bigger than the middle balloon, which is bigger than the first balloon."
Grab the smallest and the medium balloon. Hold them in one hand and hold the largest balloon in your other hand.
"Now, I have these two balloons. If I put these two balloons together (i.e. combine them) are these two balloons bigger than or smaller than this balloon?"
Shake the largest balloon in your other hand.
Smaller / About the same / Bigger / Not sure
"By how much?" Don't Know
"Now, what if I had different sized balloons even though they were in the same order would I get a different answer?" Yes
(It depends on the sizes of the two balloons chosen)
Now get a set of 3 balloons of equal size. Hold them in one hand.
"These balloons are the same size. Now I grab these two balloons."
Hold them in one hand and hold the other balloon in your other hand.
"If I put these two balloons together, combining them, are these two balloons bigger than or smaller than this balloon?"
Shake the balloon in your other hand. Bigger
"By how much?" 1 balloon
"Was that difference much easier to work out?" Yes
"Knowing the amount or quantity (or the difference between amounts / quantities - i.e. how much more or less) is the key question for measurement."
These two examples show why we need to know the intervals between our raw scores. Having equal intervals or units is also important for interpretation.( These two examples can be used as a starting point for discussions about: idealized measurement, the concepts of quantity and number, conjoint measurement, logarithmic data transformations, ogives, concatenation, frames of reference, exchangeable units, rulers and other measurement analogies - for example, balance scales, ammeters and thermometers.)
DEMONSTRATING TEST / SAMPLE DEPENDENCY
Show another set of 3 balloons: one blue, one red, one green.
 |
"Finally, I have a couple more questions to ask."
Question 1: How many balloons am I holding? 3
Question 2: How many balloons am I holding which are a primary color for painting? 2
Can you see that the sample has not changed only the question has changed?"
This example illustrates how our raw scores are based on the sample tested or the questions asked. (This example can then be used to generate further discussions about stochastic measurement and latent traits.)
"In conclusion, these examples have shown the problems with raw scores - their non-linearity, their unequal intervals, and their sample / test dependence. These problems emphasize the difference between counting and measuring. When reporting our results in the human sciences we must go beyond counting the 'correct answers' to our questions or counting the 'ordered numbers' from our rating scales. We can start to solve these issues when we think about the measurement of our variables in terms of a number line with equal interval characteristics."
Working with helium balloons is fun, though it requires a bit of practice. (I would also recommend using a classroom with low to normal ceiling height.)
References
Linacre, J. M., & Wright, B. D. (1993). Constructing linear measures from counts of qualitative observations. Paper presented at the Fourth International Conference on Bibliometrics, Informetrics and Scientometrics, Berlin, Germany, September 1993 (ERIC ED 364574).
Merbitz, C., Morris, J., & Grip, J. C. (1989). Ordinal scales and foundations of misinference. Archives of Physical Medicine and Rehabilitation, 70, 308-312.
Silverstein, B., Kilgore, K., & Fisher, W. (1989). Don't abandon FAS (Letter to the Editor in response to Merbitz, Morris & Grip 1989). Archives of Physical Medicine and Rehabilitation, 70, 864-865.
Wright, B. D. (1993). Thinking with raw scores. Rasch Measurement Transactions, 7(2), 299-300.
Wright, B. D. (1997). Fundamental measurement for outcome evaluation. Physical Medicine and Rehabilitation: State of the Art Reviews, 11(2), 261-288.
Wright, B. D., & Linacre, J. M. (1989). Observations are always ordinal: Measurements, however, must be interval. Archives of Physical Medicine and Rehabilitation, 70, 857-860.
Wright, B. D., & Mok, M. M. C. (2004). An overview of the family of Rasch Measurement Models. In E. V. Smith Jr. & R. M. Smith (Eds.), Introduction to Rasch measurement. Maple Grove, MN: JAM Press.
Nick Marosszeky
Macquarie University, Australia
Teaching Tutorial: Building Measures from Raw Scores - We Need to Use the Wright Stuff! Nick Marosszeky … Rasch Measurement Transactions, 2013, 27:2 p. 1418-21
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt272f.htm
Website: www.rasch.org/rmt/contents.htm