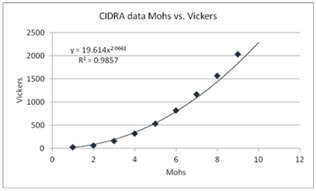
Figure 1: CIDRA data for Mohs vs. Vickers
There are three essential attributes to measuring. Rasch (1968, 1977, 2001) addressed them in various papers, and they were explicated further by Stone & Stenner (2014).
1. Comparison is primary: To compare is to distinguish: a = b; a < b; a > b.
2. Order follows: If a < b, b < c, then a < c. Transitivity results, but a test for variable monotonicity is required to establish valid order.
3. Equal Differences require a Standard Unit. A Standard Unit is established either by a personage with power (king, pope), or by agreement arising from data and consensus (science).
The process is developmental. Nothing in measuring arises full-blown. Progress occurs by steps of continued understanding resulting from intuition, reason, and improved instrumentation. We designate this encompassing process Measuring Mechanisms.
The Mohs scale of hardness is based on a scratch test mechanism. Ten key values range from talc (#1) to diamond (#10). Comparison and order are satisfied. Equal differences are not satisfied inasmuch as the difference from 7 to 8 is not the same as the difference of 3 to 4. Unequal differences occur across all the scale values. Such a scale is termed ordinal by Stevens and others embracing a level of measurement schema. While the Mohs test is a well-recognized ordinal scale, the Vickers test is another matter.
The Vickers scale is used in engineering and metallurgy operating via two different mechanisms; indentation hardness and rebound hardness. The former is determined from a microscopic device equipped with a micrometer for measuring permanent deformation of the material tested. The indentation made from an experimental indenter is carefully measured resulting in a linear numerical value that is amenable to mathematical operations.
Rebound hardness is measured from the upward "bounce" of a carefully engineered hammer descending from a fixed height (see Stone and Stenner's 2014 explication of Rasch's ashtray dropping experiment. There is similarity, but Rasch employs a purely qualitative approach to make his case). The Vickers experiment uses a scleroscope to provide a precise linear measure of rebound height. Two other related scales for measuring rebound hardness are the Leeb rebound hardness test and the Bennett hardness scale.
It would be interesting to apply and especially to compare the "hardness" of the ten key minerals on Mohs scale to an exact measure of rebound from applying the Vickers measuring mechanism. One might expect this "predicted" scale to reflect an outcome similar to a Winsteps map of items. Talc (#1) and gypsum (#2) might be calibrated close to each other because both can be scratched with the fingernail. Topaz (#8), corundum (#9), and diamond (#10) might be somewhat close together at the other end of the scale inasmuch as these three represent gemstones. The remaining minerals might be scattered, or close to one another. The map would indicate "measured" differences in hardness for the key Mohs indicators whereby some of the ten might be greatly separated and others close or similar. Extensive lists of gemstone hardness indicate that most have Mohs values of 7 and higher.
 Figure 1: CIDRA data for Mohs vs. Vickers |
CIDRA Precision Services LLC (2012) published data on mineral hardness showing the relationship of the Mohs scale to the Vickers. A plot of their data is given in Figure 1 modeled by a power curve with an R² = 0.9857. The first four values of the Mohs scale are found between zero and five hundred on the Vickers scale while the last three values on the Mohs scale show adjacent differences of about five hundred.
Oppenheimer (1956) emphasized that "Analogy is an instrument in science". He identified analogies as vital and indispensable to conducting science. Hardness measured by the Vickers test for indentation or upward bounce progresses analogously beyond (1) comparison and (2) order by providing measures of hardness whereby (3) differences are expressed on an equal interval linear scale.
So, some mechanisms yield merely ordinal relations and others quantitative relations (i.e. homogeneous differences up and down the scale). One explanation for repeated failure to engineer a mechanism sensitive to variation in homogeneous differences for an attribute is that the attribute is ordinal, however, if the history of science is any guide it may take a century or two of effort before we confidently conclude that an attribute is in some fundamental sense merely ordinal.
Mark Stone and Jack Stenner
References
CIDRA Precision Services LLC (2012). Wallingford, CT.
Oppenheimer, R. (1956). Analogy in science. American Psychologist, 11, 127-135.
Rasch, G. (1964). Objective comparisons. Lectures at the UNESCO Seminar, Voksenasen, Oslo.
Rasch, G. (1977). On specific objectivity. Danish Yearbook of Philosophy, 14, 58-94.
Rasch, G. (2001). Rasch lectures. Lina Wohik Olsen & Sven Kreiner (Eds.). Copenhagen: Copenhagen Business School.
Stone, M. & Stenner, A. J. (2014). Comparison is key. Journal of Applied Measurement, 15:1, 26-39.
From Ordinality to Quantity. M. Stone & J. Stenner … Rasch Measurement Transactions, 2014, 27:4 p. 1439-40
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt274a.htm
Website: www.rasch.org/rmt/contents.htm