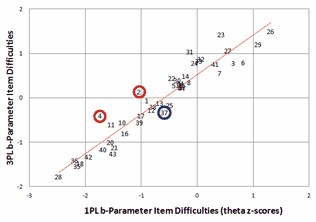
Figure 1. Plot of item difficulties from Bergan, Table 2. Person thetas are N(0,1).
Bergan (2010) states "Science entails the development of theories involving hypotheses that can be tested through the examination of data." and also "Science proceeds in exactly the opposite fashion to the Rasch approach to model selection." Bergan describes an analysis by Christine Burnham of a 44-item math test administered to 3,098 Grade 5 students. Since "An important aspect of the IRT approach is the selection of an IRT model to represent the data", the data were analyzed using 1-PL [Rasch], 2-PL and 3-PL models. Bergan's conclusion "is that for this assessment the 3PL model is preferred over the 1PL and 2PL models because the 3PL model offers a significant improvement in the fit of the model to the data over the alternative models. In other words, the additional parameters estimated in the 3PL model are justified because they help provide a better fit to the data." From the standpoint of descriptive statistics, the discussion is over, but there is more to measurement than mere description.
 Figure 1. Plot of item difficulties from Bergan, Table 2. Person thetas are N(0,1). |
Let's look more closely at these analyses. Bergan helpfully reports the item difficulties, b, according to 1PL and 3PL in his Table 2. These are plotted in our Fig. 1. The person ability theta distribution is stated to be constrained to N(0,1) in both 1PL and 3PL analyses. In the Figure, items 2 and 4 have the highest 3PL pseudo-guessing and item 37 has the lowest discrimination. Bergan attributes the average 0.5 z-score (unit-normal deviate) difference between the 1PL and 3PL estimates to the 3PL pseudo-guessing lower asymptote, c, which averages c=0.22 according to Bergan's Table 3. in particular, Bergan identifies Item 2 as more accurately estimated by 3PL than by 1PL because its pseudo-guessing lower asymptote, c, corresponds to a probability of success of 45% (c=0.45). Similar reasoning would apply to item 4 which has the highest lower asymptote, (c=0.50). Surely we are surprised by the large amount of guessing associated with these items that are targeted near the average ability level of the students. On the other hand, item 26 is the most difficult item. We could expect this item to provoke guessing by the lowest third of the sample, but its pseudo-guessing is a relatively low c=0.17.
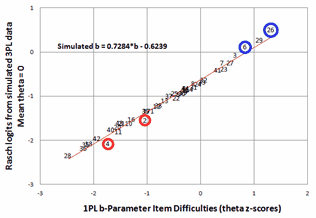 Figure 2. Plot of Rasch item difficulties estimated from data simulated with Bergan's 3PL estimates plotted against Bergan's 1PL estimates. |
In order to verify that the 1-PL analysis does correspond to a standard Rasch analysis, I simulated data using Bergan's 3-PL parameter estimates and an N(0,1) theta distribution. Rasch b-parameters for these data were estimated with Facets (chosen because its weighting capabilities allow an exact match in the data to the 3PL ogives and theta distribution). The plot of item difficulties is shown in Fig.2. The noticeable outliers are items 2 and 4 (which have high 3PL pseudo-guessing values) and items 6 and 26 (which have high 3PL discrimination). Overall, this simulation confirms that the reported 1PL analysis reasonably matches a Rasch dichotomous analysis.
More interesting are the fit statistics for the simulated items from the Rasch analysis. All the items have acceptable fit statistics! The most under-fitting item is item 37 (lowest 3PL discrimination) with an outfit mean-square of 1.13. The most over-fitting item is item 9 (which has the highest 3PL discrimination) with an outfit mean-square of 0.89. The infit mean-squares are within the range of the outfit mean-squares. Surprisingly, item 2 (high 3PL pseudo-guessing) only slightly under-fits with an outfit mean-square of 1.09, and item 4 (high 3PL pseudo-guessing) slightly over-fits due to its high 3PL discrimination. Though many simulated responses are flagged by Facets as potential guesses, they are overwhelmed in the simulation by well-behaved data and so have little influence on the Rasch fit statistics. Surprisingly, if the original data did accord with the estimated 3PL parameters, then those data would also accord with the Rasch dichotomous parameters. Bergan's comment that "In general, in science, the most parsimonious model (i.e. the model involving the least number of estimated parameters) is preferred to represent the data" would motivate the selection of Rasch over 3PL!
This advances us to the next step in any scientific investigation: quality control. A major flaw in 3PL analysis is its lack of quality-control of the data. What about item 2 with its high pseudo-guessing? Bergan admits that there can be bad items but does not describe any attempt to discover if item 2 or any other of the 44 items are bad items. Instead, he quotes Thissen and Orlando (2001) who say "The [Rasch] model is then used as a Procrustean bed that the item-response data must fit, or the item is discarded." The assumption is that item 2 fits the 3PL model and so is a good item (but no item-level fit statistics are reported to support this). The assumption is also that item 2 does not fit the Rasch model and so it would be discarded (again no item-level fit statistics are reported to support this). The simulated evidence suggests that Rasch would keep item 2, but, based on the empirical evidence, item 2 might be discarded by Rasch. Let's see why.
Bergan reports the 3PL parameter estimates in his Table 3. As we might expect, there is no correlation between 3PL item discrimination, a, and pseudo-guessing, c, and a small positive correlation, r=0.19 , between pseudo-guessing and item difficulty. There is a stronger positive correlation between item discrimination and item difficulty, r=0.33. As items become more difficult, they discriminate more strongly between high and lower performers. We might hypothesize that the more difficult items require technical knowledge of math, such as algebraic symbols, that is not taught to low performers. Thus the increase in item discrimination with difficulty could be caused by classroom teaching practices.
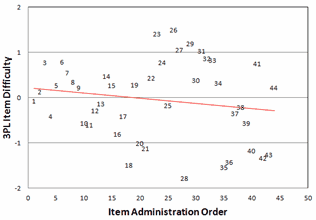 Figure 3. Plot of 3PL b item difficulty against item administration order. |
However, other correlations are more thought-provoking. Let's assume the usual situation that the 44 items are in the same order in the data as they were during the test administration. Then the correlation between item administration order and item difficulty is r = -0.17. Later items are easier overall than the earlier items. Indeed, Fig. 3 shows us that the easiest items are administered starting at item 18 of the 44 items. This is not disastrous but does contradict the folk wisdom that the easier items should be earlier in order to encourage the lower performers to do their best. We might want to point this out to the test constructors.
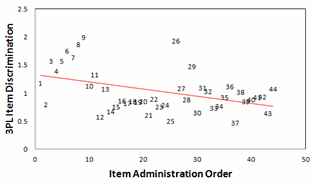 Figure 4. Plot of 3PL a item discrimination against item administration order. |
The correlation between item administration order and item discrimination is r = -0.42. We would expect a slightly positive correlation. The pattern is shown in Fig. 4. Now we do need to put on our quality-control hats. The first 9 items show a sharp increase in item discrimination. Why? And there is the unusually high discrimination of item 26. 3PL estimation algorithms usually constrain the upper limit of item discrimination. In this estimation, the maximum item discrimination appears to have been constrained to 2.0, so both item 9 (a=2.0) and item 26 (a=1.94) may actually have higher discriminations. 3PL has blindly accepted this pattern of item discrimination. Rasch analysis would flag the items with higher discriminations as over-fitting and perhaps locally dependent.
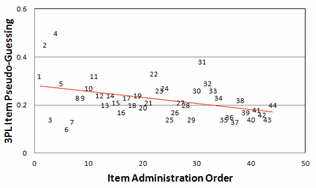 Figure 5. Plot of 3PL c item pseudo-guessing against item administration order. |
The correlation between item administration order and pseudo-guessing is r = -0.39, when we would expect a small positive correlation. The pattern is shown in Fig. 5. Now the very high pseudo-guessing for items 2 and 4 stands out. There is a definite problem at the start of the test. On the other hand, at the end of the test, when we expect guessing to increase because of time constraints, student tiredness, student frustration, etc., pseudo-guessing is, in fact, decreasing, even though items 41 and 44 are among the more difficult items.
It appears that, if we are really interested in measuring student ability, as opposed to describing a dataset, then we should seriously consider jettisoning items 2-9, 26 and perhaps one or two other items.
Bergan writes, "In the Rasch approach, data that do not fit the theory expressed in the mathematical model are ignored or discarded. In the scientific [IRT] approach, theory is discarded or modified if it is not supported by data." This view of "science" allows problematic data to control our thinking. Rasch takes a pro-active view of science. Every observation is an experiment that requires careful scrutiny. Was the experiment a success or a failure? Problematic data certainly should not be ignored, and if found to be fatally flawed must be discarded. Otherwise we risk making false inferences that could have severe repercussions throughout the academic careers of these students.
Bergan tells us, "it is expensive and risky to ignore objective data", but that is exactly what has happened in the 3PL analysis. The negative correlations and other potential aberrations in the objective data have been ignored, because the 3PL model has made no demands upon the quality of the data.
Bergan admits that "Adherence to a scientific [IRT] approach does not imply that there are no bad items. Indeed, measurement conducted in accordance with the traditional scientific approach facilitates effective item evaluation and selection." However, here it seems that 3PL does not accord with the traditional scientific approach. It fails to examine the data. It hides problems in the data, and so acts against an effective evaluation. 3PL fails as a tool of Science, but Rasch succeeds.
John Michael Linacre
References
Bergan J.R. (2010) Assessing the Relative Fit of Alternative Item Response Theory Models to the Data. Tucson AZ: Assessment Technology Inc. http://ati-online.com/pdfs/researchK12/AlternativeIRTModels.pdf
Thissen, D., & Orlando, M. (2001) Test Scoring. Mahwah, NJ: Lawrence Erlbaum Associates.
3PL, Rasch, Quality-Control and Science. J.M. Linacre … Rasch Measurement Transactions, 2014, 27:4 p. 1441-4
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt274c.htm
Website: www.rasch.org/rmt/contents.htm