Mantel-Haenszel DIF and PROX are Equivalent!

The detection of differences in item performance (DIF, Differential Item Functioning) for different groups of examinees is important if tests equivalent for these groups are to be designed and maintained.

Differential Item Performance by Mantel-Haenszel

The Mantel-Haenszel (MH) procedure (Mantel & Haenszel, 1959) is sometimes claimed to be the best method for detecting this kind of item bias (Holland & Thayer, 1986). The first step of the MH procedure is to identify two contrasting examinee groups. These are the reference group, R, chosen to provide the standard performance on the item of interest, and the focal group, F, whose differential performance, if any, is to be detected and measured.

The MH procedure requires that these groups be matched according to a relevant stratification. Since there are seldom any clear external factors by which to match the strata of these groups, implied levels of ability are used. The ability range of the groups is divided into K (usually three to five) score intervals, and these intervals are used to match samples from each group. A 2x2 contingency table for each of these K ability intervals is constructed from the responses to the suspect item by the examinees of each group. The table of responses made by the two sample groups in the jth ability interval has the form shown in the Table.

Response to Suspect Item
Group j	Right (1)	Wrong (0)	Total
Reference group	Aj (PRj1 )	Bj (PRj0 )
Focal group	Cj (PFj1 )	Dj (PFj0 )
Total			Tj

A_j is observed count. P_{R j1} is latent probability.

The MH procedure is based on estimating the probability of a member of the reference group in interval j getting the item right, P_Rj1, or getting it wrong, P_Rj0, and similarly for a member of the focal group, P_Fj1 and P_Fj0. Two statistics are derived: an estimate of the significance of the difference, and an estimate of the size of the difference. Often only the significance of the difference is reported. But, since for large samples, meaninglessly small differences can be reported as significant, the discussion here will be concerned with the estimation of the size of the difference.

The MH estimate, α, of the difference in performance on an item between the two groups across all intervals is

in which α has the range 0 to infinity, and a "no difference" null value of 1. A popular transformation of this statistic to create a symmetric scale with a null value of zero is

δ = - (4/1.7) ln(α), so that Delta = -2.35 * logit

however, δ = ln(α) is just as useful.

Holland & Thayer (1986) do not offer a useful standard error for this estimate, but subsequent work has suggested some possibilities.

Estimating the MH Estimator

The application of the MH procedure requires an understanding of what these statistics estimate. The α estimator estimates a parameter which fulfills

Since the number of ability intervals, K, is arbitrary, the parameter, α, must be kept independent of the number of levels chosen, and constant across those intervals, if it is to have meaning beyond the arbitrary stratification scheme chosen by the analyst. This condition must hold even for strata defined to contain only examinees with the same raw score, k, on the test. Thus consider the value of α_k estimated based on this interval,

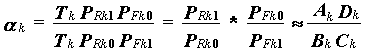
This yields the log-odds estimation equation,

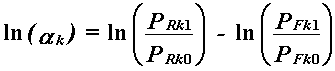
which has exactly the same mathematical features as the Rasch model, implying that MH will work successfully only on data that usefully fit the Rasch model.

The general MH relationship must also hold, in just the same way, for a score interval adjacent to j, say, h,

Both α_k and α_h estimate the same value, α. But if k and h are combined into the same interval, they must yield a third, equally valid, estimate of the same value α, namely, α_kh. Then

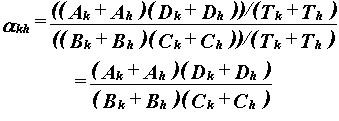
This cannot, in general, yield the same estimate of α as α_k or α_h.

If A_k=4, B_k=2, C_k=1 and D_k=2, then α_k=4. If A_h=16, B_h=4, C_h=1 and D_h=1, then α_h=4, as well.

But A_k+A_h=20, B_k+B_h=6, C_k+C_h=2, D_k+D_h=3, and so α_kh=5, which differs from α_k = α_h = 4.

The estimate of α depends in an arbitrary way on the manner in which the intervals happen to be formed by the analyst.

Parameterizing Differential Item Performance

The Rasch model specifies that each examinee has an ability, B, and each item a difficulty, D. If there is differential item performance, the item difficulty for the reference group, D_R, will be different from the item difficulty for the focal group, D_F.

Responses to items on the test, other than the suspect items, can be used to determine ability estimates for the members of both groups, and also item difficulties for all non-suspect items.

Rasch analysis yields an ability estimate, B, for each examinee in each score-group on a common interval scale. By examining performance on each suspect item, Rasch estimates can be obtained for parameters which satisfy, for each member of the reference group:

B - D_R = ln(P_R1 / P_R0)

and for each member of the focal group:

B - D_F = ln(P_F1 / P_F0)

Since Rasch objectivity places all examinees with the same raw score on the same set of items at the same ability, we can compare the performance on the suspect item of equal scoring examinees in the two groups. This gives, for a score of k,

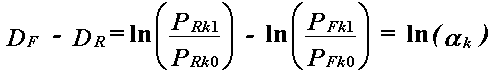
which is identical to the formulation derived for the ln(α_k) MH parameter. Thus the Rasch and MH approaches are both based on the relative odds of success of the two groups on the suspect item. The difference between the two methods is only in how this relationship is estimated and informed.

A Rasch Approach to Item Bias Detection

The item difficulty for the suspect item for the matched reference and focal groups can be estimated by the non-iterative normal approximation algorithm (PROX) (Wright and Stone, 1979 Chap. 2). Whenever a sample of person abilities can be represented by a normal distribution for the reference group, they can be subsumed into one group, j, and

D_R = M_R + X_R ln(B_j / A_j)

where D_R is the estimated difficulty of the suspect item for the reference group, M_R is the mean ability of the reference group, and X_R is a correction factor for the distribution of reference group abilities, given by sqrt(1 + V_R/2.9), with V_R being the ability variance of the reference group.

Similarly, for a sample of the focal group,

D_F = M_F + X_F ln(D_j / C_j)

Thus PROX provides estimates of D_R and D_F and so of the item bias, D_F - D_R. The model standard error of this bias is

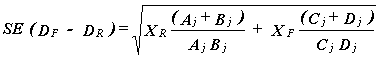
A simple test of the significance of the bias is

z = (D_F - D_R) / SE(D_F - D_R)

Thus whenever the ability distributions of the reference and focal groups are approximately normal, PROX can be used for estimating and testing the magnitude of item bias.

When data fit this Rasch model, the estimates D_F and D_R become independent of the ability composition of the reference group and focal group examinees. Consequently the comparison of D_F and D_R does not require any stratification or any matching of ability levels. Further, the estimates D_F and D_R can be calculated from all, or any convenient subset, of the reference and focal groups without any arbitrary stratification or matching. The item bias for or against the focal group is the difference between these estimates. The standard errors for D_F and D_R are well-defined and thus provide a standard error for their difference, the bias. These standard errors depend on the numbers of examinees and their ability distributions, but are independent of the size of the difference between D_F and D_R.

Comparison of MH and Rasch Approaches

The fundamental requirement of the MH procedure is that the probabilities of success for the reference and focal groups bear the same relationship across all groupings. This uniformity of relationship is required to calculate a stable estimate of the MH α statistic. But this calculation also requires the imposition of an arbitrary segmentation and matching scheme on the groups to be compared, and this arbitrary selection of interval boundaries affects the magnitude of the MH α estimate.

Rasch analysis expects the same data conditions that the MH procedure implies and requires. But, by utilizing all the relevant information from every response by reference and focal groups, Rasch analysis is able to provide a stable equivalent to the MH ln(α) statistic with an easily estimable standard error.

The Mantel-Haenszel procedure is an attempt to determine indirectly what routine Rasch analysis provides directly. The MH procedure involves theoretical uncertainties and is affected by arbitrary decisions by the analyst who uses it. If one is not prepared to accept the validity of the data under examination for Rasch analysis, then the MH procedure's implicit assumption of the stability of the relationship of the odds-ratios across ability groups will not be satisfied either. If one is prepared to accept the Rasch conditions, however, the PROX algorithm yields simpler and better defined statistics.

John M. Linacre and Benjamin D. Wright

Holland, P.W., & Thayer, D.T. (1986) Differential item performance and the Mantel-Haenszel procedure (Technical Report No. 86-69). Princeton, NJ: Educational Testing Service.

Mantel, N., & Haenszel, W. (1959) Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22, 719-748.

Wright, B.D., & Stone, M.H. (1979) Best Test Design. Chicago, IL: MESA Press.

Mantel-Haenszel DIF and PROX are Equivalent! Linacre J.M. & Wright B.D. … Rasch Measurement Transactions, 1989, 3:2 p.52-53

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt32a.htm

Website: www.rasch.org/rmt/contents.htm