Insights from National Norms: Raw Scores, Grade Equivalents and Logits, Rasch Measures
Publishers of nationally-normed achievement tests usually
provide the following information for each grade-level test of
their test series:
1. The grades to whom the grade-level test was administered
during the norming study.
2. The raw score mean and standard deviation achieved by each
grade that responded to the grade-level test.
3. For each item in the grade-level test, the proportion of the
students in each grade who made a correct response (the p-value for
the item).
In some cases the information is provided for several grades who
responded to the grade-level test. Table 1 shows a typical data
set that we compiled from this information.
Table 1
Data Set Extracted from
Published Values |
Test/Form
Level
Action |
XYZ-2
10
P2D |
Date:
File: |
02/28/1989
XYZ2‑10.p2d |
Grade
# Items
Raw Score:
Mean
S.D. |
9.1
45
25.30
9.60 |
9.7
45
28.80
9.50 |
10.1
45
30.20
9.20 |
10.7
45
31.40
9.30 |
|
Item # |
P-Value |
P-Value |
P-Value |
P-Value |
1
2
..
44
45 |
0.83
0.83
0.46
0.56 |
0.90
0.90
0.52
0.62 |
0.93
0.92
0.55
0.64 |
0.94
0.94
0.57
0.66 |
We have developed a computer program to determine from such data
the Rasch difficulties of the test items. Our purpose was to make
available to construct-definition studies a large body of observed
item difficulties. This has also given us the opportunity to
demonstrate key features of the Rasch measurement model using
published test data derived from large samples of the school
population.
We computed Rasch item difficulties for every reading
comprehension item in five of the major nationally-normed
achievement tests. We then selected grade-level tests with data
for at least four samples of students spanning at least two grades
and plotted the four or more estimates of Rasch item difficulties
for each test. Figure 1 shows one of the plots. The X-axis is the
item number and the Y-axis is the Rasch difficulty for the item in
logits, computed from the p-values. Table 2 summarizes the results
for the five tests that we analyzed.
The Rasch model is an objective measurement model, i.e., the
estimation of item difficulties is independent of the abilities of
the sample whose test data provided the basis for the estimation.
We found that, within the limits of measurement error, the
estimates of the difficulties of the items were, in fact, invariant
across groups of persons with different ability characteristics.
Table 3 shows the varying means and standard deviations of the
abilities for the groups that produced the data we analyzed.
The procedure we have developed for the estimation of Rasch item
difficulties from published p-values and raw score distributions
requires the usually reasonable assumption that the abilities in
the sample are effectively normally distributed. The variance of
raw scores is a function of the variance of the abilities of the
sample. Our procedure determines the variance in Rasch abilities
that will account for the reported variance in raw scores.
Table 2
Group RMS Differences in
Estimates of Item Difficulty from Mean |
| |
Test 1 |
Test 2 |
Test 3 |
Test 4 |
Test 5 |
Number of Groups
Number of Grades |
4
2 |
7
4 |
6
3 |
8
4 |
6
3 |
RMS Maximum
Mean
S.D. |
0.1439
0.0465
0.0299 |
0.1327
0.0459
0.0294 |
0.2168
0.0893
0.0398 |
0.2176
0.0904
0.0387 |
0.1968
0.0866
0.0352 |
We ran simulations to quantify the error in our estimates of the
standard deviation in ability at each grade. We used two sets of
item difficulties. One set had 40 items and the other set had 27.
Each of the five runs had identical input. In each case, the mean
ability was set to zero, i.e., equal to the mean item difficulty.
The "true" ability of each member of the sample was randomly
generated by a procedure that gives an approximately normal
distribution with the specified mean and standard deviation. The
response of each individual to each item was determined by
comparing the probability of a correct response to a uniformly
distributed random value. The number of correct responses then
determined the estimated ability of the person. Persons who topped
out (all correct responses) were excluded from the ability
distribution.
Error of estimation of the standard deviation of each simulated
group's ability measures was less than 0.1 logit when the test was
well-targeted on the sample, but could exceed 0.1 logit when a
large proportion of subjects achieved perfect scores.
When a large number of individuals top out, the distribution of
abilities of those whose scores contribute to p-values is truncated
at the top end, because we dropped these simulated subjects from
the analysis. This removes the upper end of the ability
distribution of the sample. In our study of the published tests,
therefore, we eliminated estimates of the standard deviation of
ability where it appeared that a test had been administered to a
group of subjects whose mean ability was too high for the test.
Table 3
Abilities of the Groups
Generating the Test Data |
| |
Group |
| Test |
Mean
(S.D.) |
Mean
(S.D.) |
Mean
(S.D.) |
Mean
(S.D.) |
Mean
(S.D.) |
Mean
(S.D.) |
Mean
(S.D.) |
Mean
(S.D.) |
1
2
3
4
5
|
0.000
(0.942)
0.000
(1.051)
0.000
(1.350)
0.000
(0.979)
0.000
(1.171) |
-0.114
(1.030)
0.454
(1.139)
0.082
(1.393)
0.080
(0.986)
0.307
(1.216) |
0.112
(0.945)
0.656
(1.150)
0.334
(1.369)
0.371
(1.076)
0.568
(1.269) |
-0.077
(1.044)
0.863
(1.245)
0.457
(1.420)
0.424
(1.054)
0.847
(1.312) |
0.879
(1.231)
0.653
(1.413)
0.598
(1.136)
0.836
(1.328) |
0.903
(1.199)
0.576
(1.395)
0.793
(1.093)
0.763
(1.324) |
0.993
(1.183)
0.883
(1.181) |
1.033
(1.171) |
We plotted the remaining estimates of the standard deviation of
abilities of the norming groups for each grade (Figure 2). Each
symbol represents a different test series. As can be seen, there
are considerable differences in the standard deviation in ability
determined from each major test. This is an effect of the
publisher's sample selection. It should also warn test user's not
to assume that a test publisher's statistics apply automatically to
the user's own situation.
The continuous line in Figure 2 represents the mean of the five
estimates of the standard deviation of abilities in each grade.
Figure 3 shows a first approximation of the mean Rasch ability in
each grade. The two outer lines show the mean ability plus and
minus one standard deviation based on the mean values from Figure
2.
We might be surprised that Figure 3 does not show the often
asserted, but never actually shown, progressive divergence of the
less able and the more able from the mean. Figure 3 does show that
the rate of increase in reading ability decreases with increasing
grade. Of course, this same Figure could be plotted using
commonly reported, but non-linear, Grade Equivalents rather than
logits. We have done this in Figure 4. The mean line becomes an
identity line, and the standard deviation lines now diverge from
the mean as grade levels increase, apparently supporting the
mistaken assertion that children become more different!
The results demonstrate that the Rasch model does produce
estimates of item difficulty that are independent of the ability
characteristics of the specific persons used to make the estimates,
and that these estimates are a better basis for inference than raw
scores or grade equivalents.
The procedures we have developed for estimating, from published
scores and p-values, Rasch item difficulties and variance in person
abilities may be applied to the similarly reported data for any
test of any construct.
Ivan Horabin, Jon Poznanski, Dean Smith
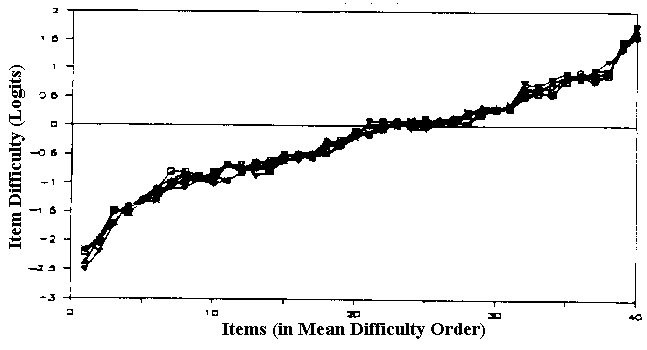
Figure 1. Item difficulties estimated from 6 groups of persons in 3 grades (Example 1).
|
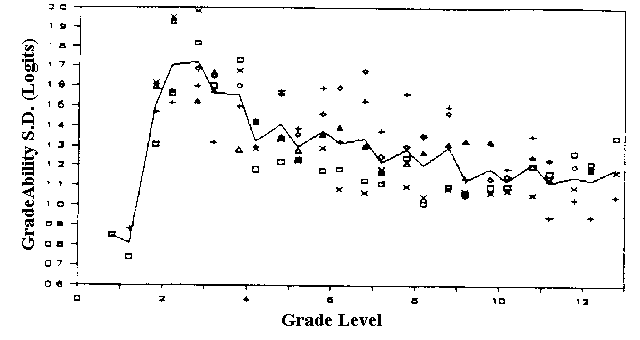
Figure 2. Estimates of the standard deviations in reading ability, by grade level,
from 5 national levels. The line indicates the mean S.D. Ability variance decreases with increasing grade.
|
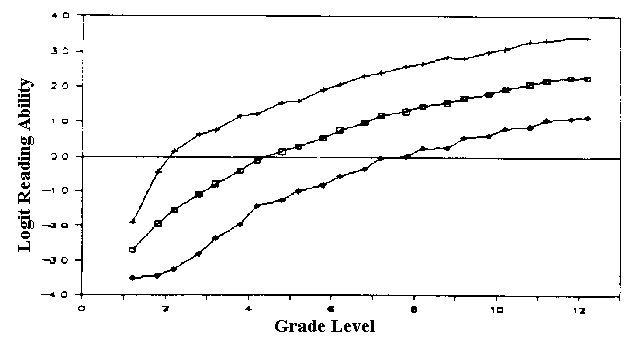
Figure 3. Mean reading ability by grade and one standard deviation from the
mean. The rate of improvement decreases with increasing grade.
|
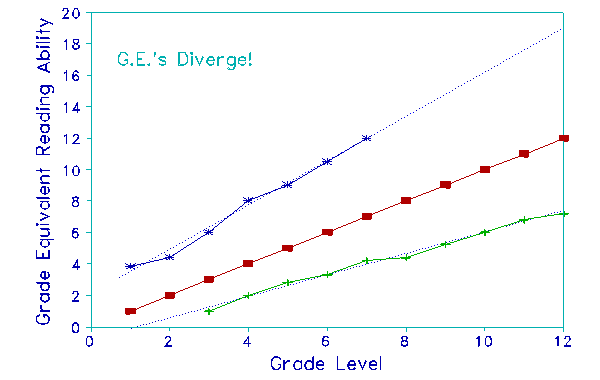
Figure 4. Grade Equivalent version of Figure 3. "---" indicates
extrapolation outside conventional G.E. range. Ability variance appears to increase
with increasing grade.
|
Insights from National Norms: Raw Scores, Grade Equivalents and Logits, Rasch Measures. Horabin I, Poznanski J, Smith D. … Rasch Measurement Transactions, 1989, 3:2 p.58-61



