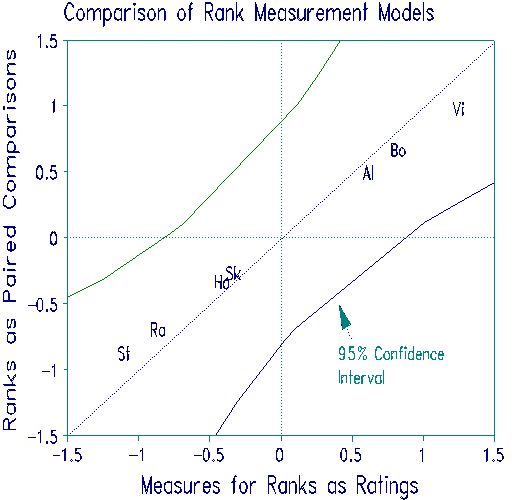
Departure from identity line has not substantive implications.
This paper is aimed at stimulating interest in Plato's emphasis on the interrelations of philosophy, education and mathematics, and does so by raising questions concerning the thesis of philosophy as this has been articulated by philosophers such as Derrida, Ricoeur, Gadamer and Levinas. Philosophy's thesis is that the metaphorical, numerical and geometrical figures that convey meaning are rigorously independent of that meaning. Of related interest is the fact that the convergence and interplay of figure and meaning in dialectical processes, and subsequent separation from one another, is fundamental to the definition of mathematical entities for the ancient Greeks. Because philosophy's thesis follows so closely from the ontology of mathematical entities, Plato required that his students have completed mathematical studies before entering the Academy. Hence, mathematics, in the wider sense of the ancients, is the fundamental metaphysical presupposition of all 'academic' knowledge, as has been pointed out by Heidegger.
Education is made possible by the existence of things that can be taught and learned, which is the same thing as saying that education follows from the thesis of philosophy. The thesis of philosophy can therefore be said to provide the structure of the educational enterprise, and this observation in turn highlights the general lack of concern for the convergence and separation of figure and meaning in educational research and practice. The educational construal of philosophy's thesis asks, "Do the order of tasks in this curriculum or test remain relatively and probabilistically constant across persons, classrooms, teachers, schools, school districts, etc.?" In order for something to be taught and learned the tasks and texts representing it must have an order of difficulty that converges with the order of the abilities persons bring to them. When such convergence is achieved, the questions and answers (or items and persons) signifying meaning fall away from that meaning such that it separates from them and takes on a life of its own--which is to say that the data fit Rasch's criteria for fundamental measurement. Despite the fact that every aspect of education requires the assumption that this convergence and separation take place, educators investigate the extent to which it occurs only rarely, but they do so quite effectively whenever Rasch's approach to measurement is employed. An example of how attention to the fundamental educational issues raised by philosophy's thesis can improve education is drawn from the work of Mark Wilson. His review of research on learning hierarchies shows how critical attention to the convergence and separation of question and answer overcomes longstanding technical and theoretical problems that raise themselves only when the role of the thesis of philosophy is ignored. Wilson shows in effect that the variations on the Guttman approach employed in this research too eagerly stresses the need for a separation of parameters without first establishing that they have converged. By organizing his research on learning hierarchies such that the data meet the requirements for measurement specified by Rasch, Wilson shows how obstinate problems in this area are overcome, how interesting and important new facts about learning are discovered/invented, and how new lines of inquiry are opened up.
The therapeutic credibility of pastoral care depends upon the demonstration of clinical efficacy in positively affecting the spiritual well-being (SWB) of patients. Although the spiritual dimension is often discussed and referred to as an established entity, little research has been done that delineates this dimension in the quantitative terms necessary for rigorous measurement, diagnostic classification, and treatment assessment. The purpose of this research is to measure SWB in a manner conducive to 1) distinguishing different levels of spiritual functioning; 2) testing the efficacy of pastoral interventions; 3) charting improved spiritual functioning; 4) assessing the possibility that further research will lead to an objective basis for recommending specific diagnostic-related treatments; and 5) relating variations in SWB to lengths of stay and outcomes. Each of these points requires instrumentation with units that will rigorously maintain their size and order free of influence from the particular patient measured or chaplain measuring; the quantitative delineation of the spiritual dimension therefore demands that our questions and experimental design be organized according to the principles of Rasch measurement. Inpatients undergoing pastoral care at a free-standing rehabilitation center are being assessed on three different forms of a new 120-item instrument in order to test the feasibility of achieving these goals.
Preliminary indications are that SWB can be measured, that different types of spiritual disfunction can be quantitatively distinguished, and that pastoral interventions are efficacious. Further research will likely lead to specific treatment recommendations, but whether high measures of SWB are associated with shorter lengths of stay and higher outcomes remains to be determined.
This study explores the test-retest consistency of computer adaptive tests of varying lengths. Examinees took two contiguous tests with the same test specifications but different items (alternate forms of varying lengths). The ability measures from the test and retest were found to correlate at .95 when attenuated for error, demonstrating that differentiation among examinee measures is comparable regardless of the length of the test or the particular subset of items. This provides evidence of the test-retest consistency of computer adaptive tests.
The subject of item bias or differential item functions has received a great deal of attention in recent years. The purpose of this study is to explore whether or not judges can validate item bias detected from statistical analysis. Judges were found to have varying levels of ability to identify the direction of bias in items. Group consensus was more successful than individual judgements. Some items were easier to classify than others. Analysis of the content and structure of items detected to have statistical bias may lead to the development of item writing rules which will produce better items.
Three examinations which require judges to assess examinee performances were analyzed to determine differences among judge severities and grading periods. An extension of the Rasch model analyzed facets for examinees, items, judges and grading periods. Significant variation in judge severities and some variations across grading periods were found on all three examinations.
Determination of the intentions of the test developer is fundamental to the choice of the analytical model for a rating scale. For confirmatory analysis, they inform the choice of the general form of the model, representing the manner in which the respondent interacts with the scale, and also of the precise statement of that form, representing the intention of the analyst to construct, say, an "equal-interval" scale. Examples of general forms and precise statements are given. Three general forms are:
1. The Andrich Model for wholistic scales
loge (Pnij/Pnij-1) = Bn - Di - Fj
where Pnij is the probability of an observation in category j, Pnij-1 is the probability of an observation in category j-1, Bn is the ability of person n, Di is the difficulty of item i, and Fj is the step difficulty or threshold between categories j and j-1, where the categories are numbered, 0,J, and all items have the same category structure. This has sufficient statistics, and bi-directional ordering of categories.
2. The Glas model for incremental scales
loge(Pnij/(1-Pnij)) = Bn - Di - Fj
for j=1,J when Xni<=j-1, where Xni is the observation from person n interacting with item i.
This has sufficient statistics, and uni-directional ordering of categories.
3. The McCullagh (also Bock, Samejima, etc) model for scales in which the category boundaries are arbitrary.
loge(sum(Pnik) / (1-sum(Pnik)) = Bn - Di - Fj
Where sum() implies the summation over k = 0, j.
This lacks sufficient statistics, but has bi-directional ordering. This paper has given rise to a discussion about what constitutes a valid measurement model for rating scales. Andrich maintains that only examples of his model in which the Fj terms are monotonically ascending constitute meaningful measurement models. The Glas model is hierarchical and may more closely match what is often referred to as "partial credit" than the Andrich model. The McCullagh model is of dubious theoretical value because of its lack of invariance, which is reflected in its statistical short-comings. It does, however, have the very useful property that combining or splitting the categories does not alter the frame of reference of the measure and calibration parameters.
Rank ordering examinees is often an easier task for judges than awarding numerical ratings. A measurement model for rankings based on Rasch's objectivity axioms provides linear, sample-independent and judge-independent measures. Estimates of examinee measures are obtained from the data set of rankings, along with standard errors and fit statistics. Judge quality-control fit statistics are also obtained for each ordering. An example is provided comparing rating and ranking of an essay examination, which indicates that from a statistical viewpoint ranking and rating are equivalent.
Critics assert that it is easier to train the novice to use a rating scale of a few categories than to discriminate between performances of very nearly equal merit in order to rank them. On the other hand, experts can already discriminate between performances, and use of a rating scale becomes an imposition.
 |
| Figure. Measures form ranks as comparisons vs. as rating. Departure from identity line has not substantive implications. |
|---|
The advantages and disadvantages of standard Rasch analysis computer programs are discussed. Sample output from a number of standard programs is examined for strong and weak points, and guidance it gives to a potential program author. Emphasis is laid on adequate and useful statistics presented as easily comprehended graphical output. Source code for a simple Rasch analysis program is provided. Though it is clear that measures, standard errors and fit statistics are always required, standard computer programs differ markedly in providing this information. Customizing the output of a standard program to make it more useful and meaningful to the intended recipients of the information is often remarkably simple, using word processing or graphical software.
AERA Paper Abstracts: Rasch, 1990 … Rasch Measurement Transactions, 1990, 4:1 p.93-95
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt41d.htm
Website: www.rasch.org/rmt/contents.htm